Bessel-I Function Calculator
Online calculator for the modified Bessel function Iv(z) of the first kind
The calculator on this page calculates the modified Bessel function Iv(z) for real numbers. Bessel functions for complex numbers can be found in the complex numbers section.
To calculate, enter the ordinal number and the argument z. Then click the 'Calculate' button. The ordinal number must be an integer and the argument z must be positive.
|
Bessel function Iv(z) of the first kind
The Bessel-I function calculates the modified Bessel function Iv(z) of the first kind. The modified Bessel functions do not exhibit oscillating but rather exponential behavior. Bessel-I (n, z) is a solution of the modified Bessel differential equation.
The result is a complex number if \(z\) is negative and \(n\) is a decimal number.
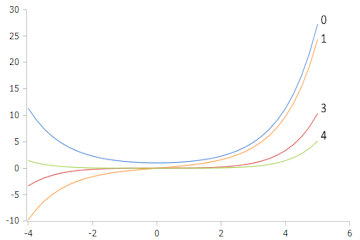
Plot of the Bessel I function with ordinal numbers 0, 1, 3 and 4
The Bessel functions are a group of special mathematical functions, which occur in various physical and mathematical applications. They were originally defined by the mathematician Daniel Bernoulli and later generalized by Friedrich Bessel. These functions are solutions of the Bessel equation for an arbitrary complex parameter \( \alpha \), which represents the order of the Bessel function.
There are two main classes of Bessel functions:
-
Bessel function of the first kind (Jα): These functions are solutions of the Bessel differential equation,
which are not singular at the origin.
They are sometimes also referred to as cylinder functions or cylinder oscillations.
- Bessel function of the second kind (Yα): In contrast to the usual Bessel functions, which oscillate as functions of a real argument, the functions \(I_\alpha\) grow exponentially, while the functions \(K_\alpha\) decay exponentially. Like the ordinary Bessel function \(J_\alpha\), the function \(I_\alpha\) approaches zero for \(x = 0\), if \( \alpha > 0 \), and is finite for \(x = 0\) if \( \alpha = 0 \).
These functions play an important role in describing vibrations of a circular membrane, electromagnetic waves in cylindrical waveguides, heat conduction in cylindrical objects, acoustic membranes (such as eardrums) and much more. They are an indispensable tool for many problems of wave propagation and static potentials in the Physics and Engineering.
IT Functions
Decimal, Hex, Bin, Octal conversion • Shift bits left or right • Set a bit • Clear a bit • Bitwise AND • Bitwise OR • Bitwise exclusive ORSpecial functions
Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann ZetaHyperbolic functions
ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • TanhTrigonometrische Funktionen
ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Degree to Radian • Radian to DegreeDefinition of the Bessel functions
Bessel functions of the first kind (Jν)
The Bessel function of the first genus of the nth order is defined as:
\(\displaystyle J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu} \)
Here \( \Gamma \) is the gamma function.
At the origin (\( z = 0 \)) these functions are finite for integer values of \( \nu \).
For non-integer values of \( \nu \) there are two linearly independent solutions.
For integer values of \( \nu \) the relationship holds:
\(\displaystyle J_{-\nu}(z) = (-1)^{\nu} J_{\nu}(z) \)
Bessel functions of the second genus (Yν)
The Bessel function of second genus nth order is defined as:
\(\displaystyle Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \ pi)} \)
Modified Bessel functions (Iν, Kν)
The modified Bessel function of the first kind of nth order is defined as:
\(\displaystyle I_{\nu}(z) = i^{-\nu} J_{\nu}(iz) \)
The modified Bessel function of the second type nth order is defined as:
\(\displaystyle K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)} \)
|
|