Description for the calculation of rhomboids
A rhomboid is a quadrangular geometric shape and has the following characteristics
It has four sides and four corners
The angles of the opposite corners are identical
The opposite sides are parallel to each other and are the same length
The diagonals have different lengths
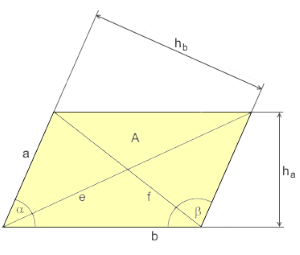
\(a\) Length
\(b\) Width
\(h_a\) Height a
\(h_b\) Height b
\(A\) Area
\(P\) Perimeter
\(e\) Long diagonal
\(f\) Short diagonal
\(α\) Angle Alpha
\(β\) Angle Beta
\(A = b · h_a\)
\(A=a · h_b\)
\(A=a · b· sin(α)\)
\(\displaystyle a = \frac{A}{h_b}\)
\(\displaystyle a = \frac{A}{b · sin(α)}\)
\(\displaystyle a = \frac{A }{ b · sin(β)}\)
\(\displaystyle b = \frac{A}{h_a}\)
\(\displaystyle b = \frac{A}{a · sin(α)}\)
\(\displaystyle b = \frac{A }{ a · sin(β)}\)
\(\displaystyle h_a = \frac{A}{b}\)
\(\displaystyle h_a = sin(α) · a\)
\(\displaystyle h_a = sin(β) · a\)
\(\displaystyle h_b = \frac{A}{a}\)
\(\displaystyle h_b= sin(α) ·b\)
\(\displaystyle h_b = sin(β) ·b\)
\(\displaystyle P = 2 ·(a + b)\)
\(\displaystyle P = 2 · \frac{h_a}{sin(α)} + (2 · b)\)
\(\displaystyle e = \sqrt{a^2 + b^2 - 2 · a · b · cos(β)}\)
\(\displaystyle f = \sqrt{a^2 + b^2; - 2 · a · b · cos(α)}\)
\(\displaystyle α = asin\left(\frac{A}{a · b}\right)\)