18dB Crossover
Calculation of a 3rd order loudspeaker crossover with 18dB attenuation per octave
Crossover Calculator
18dB Crossover (3rd Order)
Professional crossover with three components per way for maximum separation. Attenuation: 18dB per octave (Butterworth characteristic).
Circuit Diagram
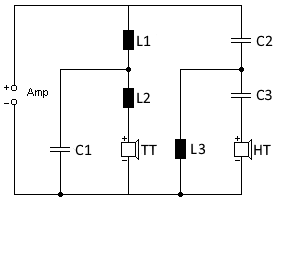
Circuit diagram of an 18dB crossover (3rd order)
The calculated values are automatically inserted into the circuit diagram. 3rd order requires 3 components per way.
|
|
|
|
Low-pass Formulas
Inductor L₁
Inductor L₂
Capacitor C₁
High-pass Formulas
Capacitor C₂
Capacitor C₃
Inductor L₃
Variable Legend
| \(L_1, L_2, L_3\) | Inductors (Henry) |
| \(C_1, C_2, C_3\) | Capacitors (Farad) |
| \(Z\) | Impedance (Ohm) |
| \(f_C\) | Crossover frequency (Hz) |
| \(\pi\) | Pi ≈ 3.14159 |
Important Note
With 18dB crossovers, polarity reversal of one speaker is required, as the phase rotation is 360°.
Filter Characteristics
Butterworth Filter
Best compromise between amplitude and phase. Maximally flat response in passband.
Bessel Filter
Optimal phase behavior and transient response, but worse amplitude behavior.
Chebyshev Filter
Best amplitude behavior, but worse transient and phase behavior.
Characteristics of 18dB Crossover (3rd Order)
Operation
A 3rd order crossover requires 3 components in each branch and provides a slope steepness of 18dB per octave. The attenuation at the crossover frequency is 3dB. This crossover is based on the Butterworth characteristic and represents the optimal compromise between amplitude and phase behavior.
Advantages
- Very steep separation (18dB/octave)
- Minimal frequency overlap
- Professional applications
- Precise frequency separation
Disadvantages
- Many components required
- High costs
- Complex circuit
- Polarity reversal required
Technical Details
Phase Behavior
The phase rotates from 0° to 360° depending on frequency. At the crossover frequency the phase rotation is 270°, which requires polarity reversal of one speaker.
Butterworth Characteristic
The 18dB crossover uses the Butterworth characteristic as optimal compromise between different filter types. 3dB attenuation at crossover frequency.
Typical Application
18dB crossovers are used in professional applications where maximum frequency separation is more important than simple installation.
Low-pass Calculation Example
Given: 8Ω speaker, crossover frequency 2400Hz
\[L_1 = \frac{3 \times 8Ω}{4π \times 2400Hz} ≈ 0.80\text{ mH}\]
\[L_2 = \frac{8Ω}{4π \times 2400Hz} ≈ 0.27\text{ mH}\]
\[C_1 = \frac{2}{3π \times 2400Hz \times 8Ω} ≈ 11.1\text{ µF}\]
Comparison of Crossover Orders
| Order | Attenuation | Components per way | Phase behavior | Application |
|---|---|---|---|---|
| 1st order | 6dB/octave | 1 (L or C) | Polarity reversal needed | Simple systems |
| 2nd order | 12dB/octave | 2 (L and C) | No polarity reversal | HiFi standard |
| 3rd order | 18dB/octave | 3 (L-C-L or C-L-C) | Polarity reversal needed | Professional |
Filter Characteristics in Detail
Butterworth
Advantages: Flat frequency response, good compromise
Disadvantages: Medium phase behavior
Bessel
Advantages: Best phase behavior
Disadvantages: Less steep slopes
Chebyshev
Advantages: Steepest slopes
Disadvantages: Ripple in passband
|
|