Activity Selection Problem
Calculator for optimal scheduling of activities (ISMP)
Interval Scheduling Maximization Problem: Find the maximum number of non-overlapping activities
Activity Selection Calculator
Activity Selection Problem
The activity selection problem determines the maximum number of activities that can be performed without time overlap.
Scheduling Visualization
Example: Default Data

Timeline representation of activities
Optimal selection without overlaps
Greedy Algorithm
- Sort by finish times
- Select earliest finish time
- Skip overlapping activities
- Repeat until all checked
|
|
Greedy Algorithm for Activity Selection
The greedy algorithm solves the activity selection problem optimally through a simple strategy:
Step 1: Sorting
Order activities by ascending finish times
Step 2: Greedy Selection
No overlap with last selected activity
Mathematical Formulation and Examples
Problem Definition
Maximize the number of selected activities without overlap
Greedy Algorithm Pseudocode
Time complexity: O(n log n) for sorting + O(n) for selection
Step-by-Step Example
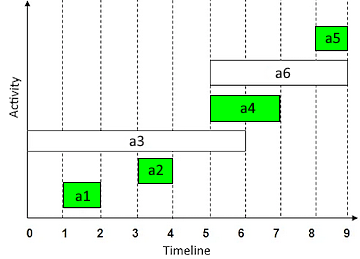
Given: Activities with start and finish times
| Activity | Start time (s) | Finish time (f) | Duration |
|---|---|---|---|
| A₁ | 1 | 2 | 1 |
| A₂ | 3 | 4 | 1 |
| A₃ | 0 | 6 | 6 |
| A₄ | 5 | 7 | 2 |
| A₅ | 8 | 9 | 1 |
| A₆ | 5 | 9 | 4 |
Solution steps:
1. Sort by finish times: A₁(f=2) → A₂(f=4) → A₃(f=6) → A₄(f=7) → A₅(f=9) → A₆(f=9)
2. Select A₁: finish time = 2
3. Check A₂: start(3) ≥ 2 ✓ → select A₂, finish time = 4
4. Check A₃: start(0) < 4 ✗ → skip
5. Check A₄: start(5) ≥ 4 ✓ → select A₄, finish time = 7
6. Check A₅: start(8) ≥ 7 ✓ → select A₅, finish time = 9
7. Check A₆: start(5) < 7 ✗ → skip
Result: {A₁, A₂, A₄, A₅} - 4 activities
Optimality Proof (Greedy Choice Property)
Theorem: The greedy algorithm (earliest finish first) delivers an optimal solution.
Proof: Let A* be an optimal solution and A the greedy solution. If the first activity in A* does not have the earliest finish time, it can be replaced by the earliest one without losing optimality.
Activity Selection Reference
Default Example
Complexity
Time: O(n log n)
Space: O(1)
Sorting: O(n log n)
Selection: O(n)
Greedy Strategies
✓ Earliest finish time: optimal
✗ Shortest duration: not optimal
✗ Fewest conflicts: not optimal
✗ Earliest start time: not optimal
Applications
Scheduling: resource planning
Rooms: room allocation
Machines: machine utilization
Events: event planning
Activity Selection Problem - Detailed Description
Problem Definition
The activity selection problem is a classic optimization problem in computer science and operations research. Given n activities with respective start and finish times, the goal is to select the maximum number of activities that do not overlap in time.
• Activity i: start time s_i, finish time f_i
• Two activities overlap if their time intervals intersect
• Goal: Maximize |S| with S ⊆ {1,2,...,n}
• Constraint: No two activities in S overlap
Greedy Algorithm
The greedy algorithm solves the problem optimally through a simple heuristic: Always choose the activity with the earliest finish time that does not conflict with already selected activities. This strategy is surprisingly optimal.
Why "Earliest Finish Time"?
An activity with an earlier finish time leaves more room for future activities. This maximizes the choices for the remaining time.
Practical Applications
Activity Selection is used in many real scheduling problems: from room allocation at universities to machine utilization in factories to optimal use of broadcast frequencies.
• Conference room bookings
• Production planning
• Personnel shift scheduling
• Resource allocation
Algorithm Analysis
The time complexity of the algorithm is mainly determined by sorting the activities by finish times: O(n log n). The actual selection occurs in linear time O(n).
Optimality Proof
The proof of optimality uses an exchange argument: Every optimal solution can be transformed into a greedy solution without reducing the number of selected activities.
Practical Examples and Variants
Conference Room Scheduling
Problem: schedule meetings optimally
Input: meeting times
Solution: maximum meetings
Benefit: room efficiency
Machine Scheduling
Problem: jobs on machine
Input: processing times
Solution: maximum utilization
Benefit: throughput optimization
Frequency Allocation
Problem: distribute transmission slots
Input: transmission times
Solution: interference-free
Benefit: spectrum efficiency
Extended Variants
- Weighted problem: activities have different priorities
- Multi-machine: multiple parallel resources
- Online version: activities arrive sequentially
- Deadlines: activities have hard deadlines
- Setup times: changeover times between activities
- Resource constraints: additional resource limitations
|
|
|
|