Birthday Paradox Calculator
Online calculator to compute the birthday paradox probability
Birthday Paradox Calculator
The Birthday Paradox
The birthday paradox describes the surprisingly high probability that in a group of n people at least two share the same birthday.
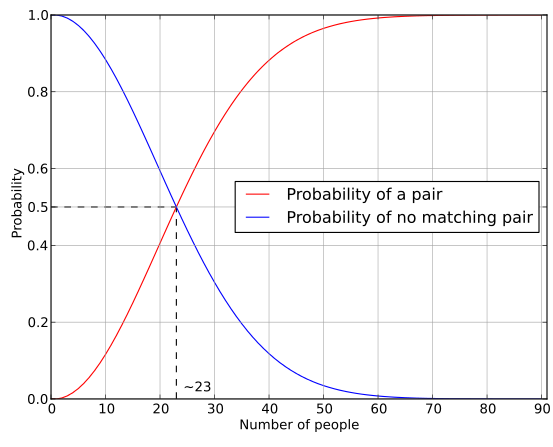
Probability Curve
The probability increases quickly with the group size.
At23 people it already exceeds50%.
? At least two same birthdays
? All birthdays different
|
|
What is the Birthday Paradox?
The birthday paradox is one of the best-known examples of counterintuitive probabilities:
- Definition: Probability that at least two people in a group share the same birthday
- Paradox: The probability is much higher than intuitively expected
- Magic number: Already above50% at23 people
- Applications: Cryptography, hashing, collision detection
- Principle: Exponential growth of the number of pairs
- Related: Coupon collector problem, birthday attack
Why is the probability so high?
The high probability is explained by the exponential growth of the number of pairs:
Number of pairs
- 2 people:1 pair to compare
- 3 people:3 pairs to compare
- 23 people:253 pairs to compare
- n people: n(n-1)/2 pairs
Probability milestones
- 10 people: ?11.7% probability
- 20 people: ?41.1% probability
- 23 people: ?50.7% probability
- 30 people: ?70.6% probability
Applications of the Birthday Paradox
The birthday paradox has important practical applications:
Cryptography & Security
- Birthday attacks on hash functions
- Collision detection in encryption
- Vulnerability analysis of algorithms
- Random number generator tests
Computer Science & Data Processing
- Hash table design and optimization
- Duplicate detection in large datasets
- Load-balancing algorithms
- Probabilistic data structures
Statistics & Research
- Sample size determination
- Random experiments and Monte Carlo methods
- Probability education and teaching
- Empirical validation of theories
Practical applications
- Quality control in manufacturing
- Scheduling and resource management
- Risk assessment in insurance
- Network traffic analysis
Formulas for the Birthday Paradox
Basic relation
Complementary probability
All different birthdays
Probability that n birthdays are all different
Product formula
Stepwise calculation for all different birthdays
Compact product form
Product notation with index
Approximation (Stirling)
Approximation for large n
50% threshold
Estimate for50% probability
Example calculations for the Birthday Paradox
Example1:3 people
Step1: All different birthdays
Step2: At least one match
Example2:23 people (The magic number)
Product calculation
Paradox result
Example3:50 people
Use approximation
Impressive result
Probability table
| People | Pairs | Probability | People | Pairs | Probability |
|---|---|---|---|---|---|
| 10 | 45 | 11.7% | 40 | 780 | 89.1% |
| 15 | 105 | 25.3% | 50 | 1225 | 97.0% |
| 23 | 253 | 50.7% | 60 | 1770 | 99.4% |
| 30 | 435 | 70.6% | 70 | 2415 | 99.9% |
Mathematical foundations of the Birthday Paradox
The birthday paradox is a classic example of counterintuitive probabilities and vividly demonstrates how the human mind struggles to assess exponential growth effects. It is based on combinatorial principles and the computation of complementary probabilities.
Combinatorial basics
The paradox relies on the combinatorial analysis of possible birthday distributions:
- Number of pairs: For n people there are \(\binom{n}{2} = \frac{n(n-1)}{2}\) pairs to compare
- Quadratic growth: The number of comparisons grows quadratically with the number of people
- Complementary event: It is easier to compute the probability that all birthdays are different
- Product rule: Probabilities of independent events are multiplied
- Normalization:365 possible birthdays assuming no leap years
Why is it paradoxical?
Most people drastically underestimate the probability for several reasons:
Cognitive biases
People think linearly rather than exponentially and overestimate the importance of365 possible days instead of focusing on the number of pairs.
Wrong analogy
Confusing with the question "How likely is someone to be born on MY birthday?" (much lower probability).
Underestimating combinatorics
The quadratic increase in pair comparisons is not intuitively captured. With23 people there are already253 pairwise comparisons.
Neglecting small probabilities
Each pair comparison has a small collision probability, but the accumulation over all pairs results in a high total probability.
|
|
|
|