Geburtstagsparadoxon Rechner
Online Rechner zur Berechnung des Geburtstagsparadoxons
Geburtstagsparadoxon Rechner
Das Geburtstagsparadoxon
Das Geburtstagsparadoxon beschreibt die überraschend hohe Wahrscheinlichkeit, dass in einer Gruppe von n Personen mindestens zwei am selben Tag Geburtstag haben.
Wahrscheinlichkeitsverlauf
Die Wahrscheinlichkeit steigt exponentiell mit der Gruppengröße.
Bereits bei 23 Personen liegt sie über 50%.
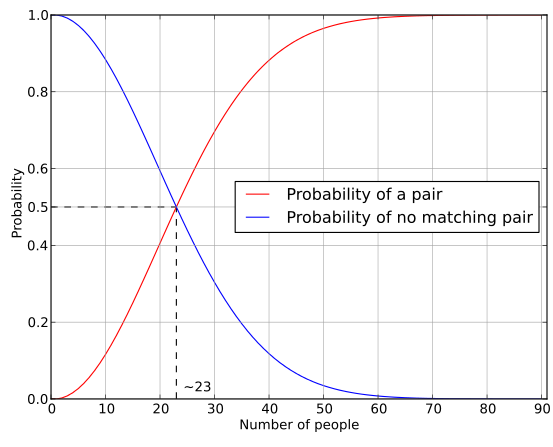
● Mindestens zwei gleiche Geburtstage
● Alle verschiedene Geburtstage
|
|
Was ist das Geburtstagsparadoxon?
Das Geburtstagsparadoxon ist eines der bekanntesten Beispiele für kontraintuitive Wahrscheinlichkeiten:
- Definition: Wahrscheinlichkeit, dass in einer Gruppe mindestens zwei Personen am selben Tag Geburtstag haben
- Paradox: Die Wahrscheinlichkeit ist viel höher als intuitiv erwartet
- Magische Zahl: Bei 23 Personen bereits über 50% Wahrscheinlichkeit
- Anwendung: Kryptographie, Hashing, Kollisionserkennung
- Prinzip: Exponentielles Wachstum der Paaranzahl
- Verwandt: Coupon-Collector-Problem, Geburtstagsangriff
Warum ist die Wahrscheinlichkeit so hoch?
Die hohe Wahrscheinlichkeit erklärt sich durch das exponentielle Wachstum der Paaranzahl:
Anzahl der Paare
- 2 Personen: 1 Paar zu vergleichen
- 3 Personen: 3 Paare zu vergleichen
- 23 Personen: 253 Paare zu vergleichen
- n Personen: n(n-1)/2 Paare
Wahrscheinlichkeits-Meilensteine
- 10 Personen: ≈ 11.7% Wahrscheinlichkeit
- 20 Personen: ≈ 41.1% Wahrscheinlichkeit
- 23 Personen: ≈ 50.7% Wahrscheinlichkeit
- 30 Personen: ≈ 70.6% Wahrscheinlichkeit
Anwendungen des Geburtstagsparadoxons
Das Geburtstagsparadoxon hat wichtige praktische Anwendungen:
Kryptographie & Sicherheit
- Geburtstagsangriffe auf Hash-Funktionen
- Kollisionserkennung in Verschlüsselung
- Schwachstellen-Analyse von Algorithmen
- Zufallszahlengenerator-Tests
Informatik & Datenverarbeitung
- Hash-Tabellen-Design und -Optimierung
- Duplikatserkennung in großen Datenmengen
- Load-Balancing-Algorithmen
- Probabilistische Datenstrukturen
Statistik & Forschung
- Stichprobengrößen-Bestimmung
- Zufallsexperimente und Monte-Carlo-Methoden
- Wahrscheinlichkeitsunterricht und -education
- Empirische Validierung von Theorien
Praktische Anwendungen
- Qualitätskontrolle in der Produktion
- Terminplanung und Ressourcenmanagement
- Risikobewertung in Versicherungen
- Netzwerk-Traffic-Analyse
Formeln für das Geburtstagsparadoxon
Grundformel
Komplementäre Wahrscheinlichkeit
Alle verschiedene Geburtstage
Wahrscheinlichkeit für n verschiedene Geburtstage
Produktformel
Schrittweise Berechnung für alle verschiedene Geburtstage
Kompakte Produktform
Produktschreibweise mit Index
Approximation (Stirling)
Näherungsformel für große n
50%-Schwelle
Abschätzung für 50% Wahrscheinlichkeit
Beispielrechnungen für das Geburtstagsparadoxon
Beispiel 1: 3 Personen
Schritt 1: Alle verschiedene Geburtstage
Schritt 2: Mindestens eine Übereinstimmung
Beispiel 2: 23 Personen (Die magische Zahl)
Produktberechnung
Paradoxon-Ergebnis
Beispiel 3: 50 Personen
Approximation verwenden
Beeindruckendes Ergebnis
Wahrscheinlichkeits-Tabelle
| Personen | Paare | Wahrscheinlichkeit | Personen | Paare | Wahrscheinlichkeit |
|---|---|---|---|---|---|
| 10 | 45 | 11.7% | 40 | 780 | 89.1% |
| 15 | 105 | 25.3% | 50 | 1225 | 97.0% |
| 23 | 253 | 50.7% | 60 | 1770 | 99.4% |
| 30 | 435 | 70.6% | 70 | 2415 | 99.9% |
Mathematische Grundlagen des Geburtstagsparadoxons
Das Geburtstagsparadoxon ist ein klassisches Beispiel für kontraintuitive Wahrscheinlichkeiten und demonstriert eindrucksvoll, wie schwer das menschliche Gehirn exponentielle Wachstumseffekte einschätzen kann. Es basiert auf kombinatorischen Prinzipien und der Berechnung komplementärer Wahrscheinlichkeiten.
Kombinatorische Grundlagen
Das Paradoxon beruht auf der kombinatorischen Analyse der möglichen Geburtstagsverteilungen:
- Paaranzahl: Bei n Personen gibt es \(\binom{n}{2} = \frac{n(n-1)}{2}\) Paare zu vergleichen
- Exponentieller Anstieg: Die Anzahl der Vergleiche wächst quadratisch mit der Personenzahl
- Komplementärereignis: Es ist einfacher, die Wahrscheinlichkeit für alle verschiedene Geburtstage zu berechnen
- Produktregel: Wahrscheinlichkeiten unabhängiger Ereignisse werden multipliziert
- Normalisierung: 365 mögliche Geburtstage bei Vernachlässigung von Schaltjahren
Warum ist es paradox?
Die meisten Menschen unterschätzen die Wahrscheinlichkeit drastisch aus mehreren Gründen:
Kognitive Verzerrungen
Menschen denken linear statt exponentiell und überschätzen die Bedeutung der 365 möglichen Tage, statt sich auf die Paaranzahl zu konzentrieren.
Falsche Analogie
Verwechslung mit der Frage "Wie wahrscheinlich ist es, dass jemand an MEINEM Geburtstag geboren wurde?" (deutlich geringere Wahrscheinlichkeit).
Unterschätzung der Kombinatorik
Die quadratische Zunahme der Paarvergleiche wird intuitiv nicht erfasst. Bei 23 Personen sind bereits 253 Paarvergleiche nötig.
Vernachlässigung kleiner Wahrscheinlichkeiten
Jeder einzelne Paarvergleich hat nur eine kleine Kollisionswahrscheinlichkeit, aber die Kumulation über alle Paare führt zu hohen Gesamtwahrscheinlichkeiten.
Mathematische Varianten und Erweiterungen
Das Geburtstagsparadoxon lässt sich in verschiedene Richtungen verallgemeinern:
Verallgemeinerte Versionen
Statt 365 Tagen kann man beliebige Anzahlen von "Fächern" betrachten. Die allgemeine Formel für d Tage und n Personen: \(P(n,d) = 1 - \prod_{i=0}^{n-1} \frac{d-i}{d}\)
Starkes Geburtstagsparadoxon
Fragt nach der Wahrscheinlichkeit, dass mindestens drei Personen am selben Tag Geburtstag haben. Dies erfordert komplexere kombinatorische Rechnungen.
Coupon-Collector-Problem
Verwandtes Problem: Wie viele Personen braucht man, um mit hoher Wahrscheinlichkeit alle 365 Tage "abzudecken"? Antwort: etwa 2287 Personen für 95% Wahrscheinlichkeit.
Approximationen
Für große d und moderate n: \(P(n,d) \approx 1 - e^{-\frac{n^2}{2d}}\). Diese Approximation ist für das klassische Problem sehr genau.
Praktische Bedeutung in der Informatik
Das Geburtstagsparadoxon hat fundamentale Bedeutung für die Informatik:
Hash-Funktionen
Bestimmt die erwartete Anzahl von Eingaben, bis eine Kollision auftritt. Bei einer n-Bit Hash-Funktion erwartet man Kollisionen nach etwa \(2^{n/2}\) Versuchen.
Kryptographische Sicherheit
Geburtstagsangriffe nutzen das Paradoxon, um Kollisionen in kryptographischen Hash-Funktionen zu finden und damit deren Sicherheit zu kompromittieren.
Datenstrukturen
Design von Hash-Tabellen muss das Geburtstagsparadoxon berücksichtigen, um eine gleichmäßige Verteilung und geringe Kollisionsraten zu gewährleisten.
Zufallszahlen-Tests
Prüfung der Qualität von Pseudozufallszahlengeneratoren durch Analyse der Kollisionsrate bei wiederholten Stichproben.
Didaktische Aspekte
Lehrwert
Das Paradoxon ist ein hervorragendes Beispiel für die Diskrepanz zwischen Intuition und mathematischer Realität. Es lehrt die Bedeutung systematischer Analyse gegenüber intuitivem Schätzen.
Experimentelle Verifikation
Lässt sich leicht durch Simulation oder empirische Experimente (z.B. in Schulklassen) verifizieren, was das Verständnis für probabilistische Phänomene fördert.
Historische Entwicklung
Entstehungsgeschichte
Erstmals formuliert von Richard von Mises (1939), popularisiert durch Harold Davenport und Richard Bellman in den 1950er Jahren.
Moderne Relevanz
Mit dem Aufkommen der Computertechnik gewann das Paradoxon neue Bedeutung in der Kryptographie und algorithmischen Komplexitätstheorie.
Zusammenfassung
Das Geburtstagsparadoxon ist weit mehr als nur eine mathematische Kuriosität. Es demonstriert fundamentale Prinzipien der Wahrscheinlichkeitstheorie, hat praktische Anwendungen in der Informatik und Kryptographie und dient als wichtiges Lehrbeispiel für die Grenzen menschlicher Intuition bei probabilistischen Phänomenen. Das Verständnis des Paradoxons ist essentiell für jeden, der sich mit Wahrscheinlichkeiten, Kombinatorik oder angewandter Informatik beschäftigt.
|
|
|
|