Beta Functions

Description of the beta function

The function \(Beta\) (Euler's beta function), also Euler's integral type 1 is a mathematical function of two complex numbers. Their definition is:

\(\displaystyle Beta(a,b) = \int_0^1 t^{a-1}(1-t)^{b-1} dt \)

\(Beta\) calculates the beta function for the arguments \(a \) and \(b \). The arguments must be real and 0 or positive.

You can also use a list in one of the parameters.

Syntax

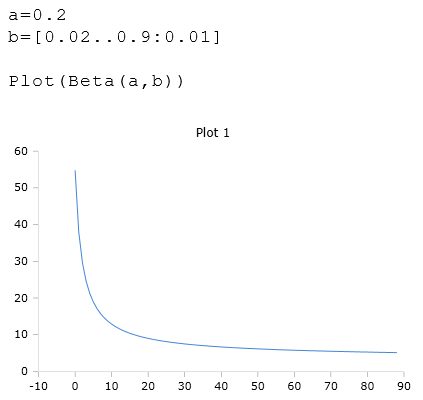
Beta (a, b)

Beispiel

IBeta Function

The function \(IBeta \) calculates the incomplete regulated beta function for the arguments \(a \) and \(b \). The arguments must be real and 0 or positive.

One of the arguments can also be a list of real numbers.

The parameter \(x\) is the upper bound of the integral in the range: \(1 >= x >= 0\)

Syntax

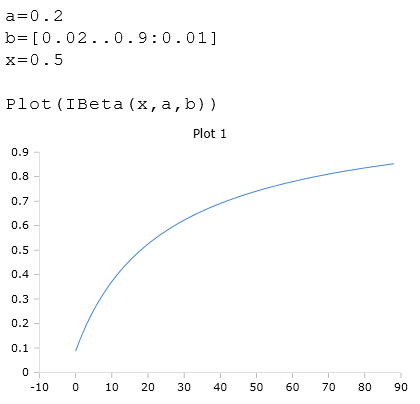
IBeta(x, a, b)

Example