Beta Funktionen
Eulersche Betafunktionen
Beschreibung der Beta Funktion
Die Funktion \(Beta\) (Eulersche Betafunktion), auch Eulersches Integral 1. Art ist eine mathematische Funktion zweier komplexer Zahlen. Ihre Definition lautet:
\(\displaystyle Beta(a,b) = \int_0^1 t^{a-1}(1-t)^{b-1} dt \)
\(Beta\) berechnet die Beta-Funktion für die Argumente \(a\) und \(b\). Die Argumente müssen reell und 0 oder positiv sein.
In einem der Parameter kann auch eine Listen eingesetzt werden.
Syntax
Beta (a, b)
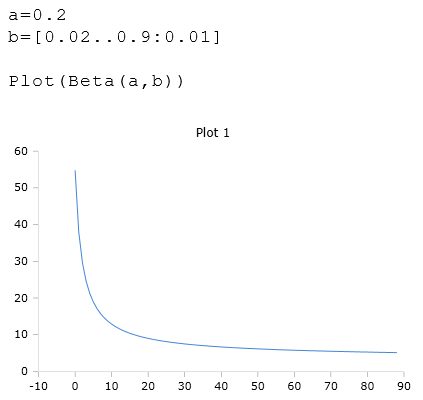
Beispiel
IBeta Funktion
Die Funktion \(IBeta\) berechnet die unvollständige regulierte Beta-Funktion für die Argumente \(a\) und \(b\). Die Argumente müssen reell und 0 oder positiv sein. Eines der Argumente kann auch eine Liste reeller Zahlen sein.
Der Parameter \(x\) ist die obere Grenze des Integrals im Bereich: \(1 >= x >= 0\)
Syntax
IBeta(x, a, b)
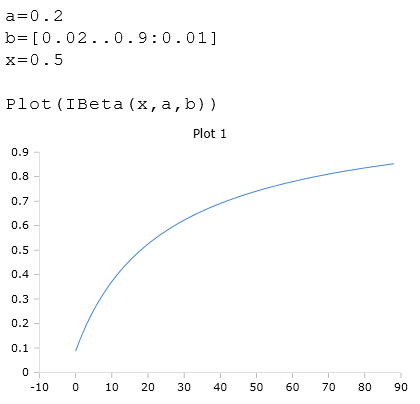
Beispiel
|
|