Error Function Calculator

Online calculator for computing the error function erf(x)

Error Function Calculator

The Error Function

The error function erf(x) is an important special function used in statistics, probability theory and engineering.

Enter Parameters
Input argument x (typically -5 to 5)
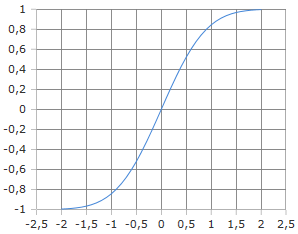
Error Function Result
erf(x):
Error function value
Error Function Properties

Range: -1 ≤ erf(x) ≤ 1, Odd function with erf(0) = 0

-1 ≤ erf(x) ≤1 Odd function erf(0) = 0

Error Function Curve

The error function approximates a sigmoid behavior.
Rapid transition from -1 to +1 around x = 0.

Error Function

What is the Error Function?

The error function erf(x) is a fundamental mathematical function:

  • Definition: erf(x) = (2/√π) ∫₀ˣ e^(-t²) dt
  • Range: -1 ≤ erf(x) ≤ 1
  • Odd function: erf(-x) = -erf(x)
  • Application: Statistics, probability, heat transfer, quantum mechanics
  • Related to: Normal distribution, complementary error function erfc(x)
  • Properties: Smooth, monotonically increasing, differentiable

Properties and Relationships

The error function has important mathematical properties:

Key Properties
  • Odd symmetry: erf(-x) = -erf(x)
  • Boundary values: erf(0) = 0, erf(∞) = 1
  • Derivative: d/dx[erf(x)] = (2/√π)e^(-x²)
  • Taylor series: erf(x) = (2/√π)Σ(-1)ⁿx^(2n+1)/(n!(2n+1))
Related Functions
  • Complementary error: erfc(x) = 1 - erf(x)
  • Relationship: erf(x) + erfc(x) = 1
  • Scaled error: erfcx(x) = e^(x²)erfc(x)
  • Imaginary error: erfi(x) = -i·erf(ix)

Applications of the Error Function

The error function is used in many scientific and engineering fields:

Statistics & Probability
  • Normal distribution CDF calculation
  • Confidence intervals
  • Statistical hypothesis testing
  • Probability density computations
Physics & Engineering
  • Heat diffusion equations
  • Diffusion processes
  • Quantum mechanical wave functions
  • Signal processing filters
Science & Measurement
  • Error analysis in measurements
  • Uncertainty quantification
  • Calibration curves
  • Instrumental precision
Numerical Methods
  • Approximation algorithms
  • Series expansions
  • Continued fractions
  • Computational efficiency

Formulas for the Error Function

Error Function (Integral Definition)
\[erf(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} dt\]

Standard integral definition with Gaussian form

Complementary Error Function
\[erfc(x) = 1 - erf(x) = \frac{2}{\sqrt{\pi}} \int_x^{\infty} e^{-t^2} dt\]

Tail probability of normal distribution

Taylor Series
\[erf(x) = \frac{2}{\sqrt{\pi}} \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{n!(2n+1)}\]

Power series expansion around x = 0

Derivative
\[\frac{d}{dx}erf(x) = \frac{2}{\sqrt{\pi}} e^{-x^2}\]

Derivative is a Gaussian function

Inverse Error Function
\[x = erf^{-1}(y), \quad -1 < y < 1\]

Inverse function for finding argument from value

Asymptotic Expansion (Large x)
\[erf(x) \approx 1 - \frac{e^{-x^2}}{\sqrt{\pi}x} \quad \text{for large } x\]

Approximation for large argument values

Example Calculations for the Error Function

Example1: Normal Distribution CDF
Standard normal, P(Z ≤1)
Relationship to Normal Distribution
  • Standard normal: N(0,1)
  • Find: P(Z ≤ 1)
  • Relationship: P(Z ≤ x) = [1 + erf(x/√2)]/2
Calculation: P(Z ≤1) = [1 + erf(1/√2)]/2
Solution
\[erf(1/\sqrt{2}) = erf(0.7071) \approx 0.6827\] \[P(Z \leq 1) = \frac{1 + 0.6827}{2} = 0.8414\] \[= 84.14\%\]
Interpretation: About 84.14% of a standard normal distribution falls below 1 standard deviation above the mean.
Example2: Heat Diffusion
Semi-infinite medium, x =0.5, α·t/L² =0.5
Physical Problem
  • Heat diffusion in semi-infinite medium
  • Temperature profile at depth x
  • Solution involves complementary error function
Formula: T = T₀ + (T₁ - T₀)erfc(η)
Calculation
\[\eta = \frac{x}{2\sqrt{\alpha t}} = 0.5\] \[erfc(0.5) = 1 - erf(0.5)\] \[= 1 - 0.5205 = 0.4795\]
Application: Error function solves transient heat conduction problems.
Example3: Calculator Default Value
x = 0.5
Direct Calculation
\[erf(0.5) = \frac{2}{\sqrt{\pi}} \int_0^{0.5} e^{-t^2} dt\] \[\approx 0.5205\]
Related Values
\[erfc(0.5) = 1 - 0.5205 = 0.4795\] \[\frac{d}{dx}erf(x)\bigg|_{x=0.5} \approx 0.8788\]
Error Function Values
x erf(x) erfc(x) Approx. %-ile
0.00.00001.000050.00%
0.50.52050.479569.85%
1.00.84270.157384.27%
1.50.96610.033993.31%
2.00.99530.004797.73%
2.50.99990.000199.38%

Mathematical Foundations of the Error Function

The error function is a fundamental special function in mathematics that arises naturally in probability theory, statistics, and the solution of differential equations. It represents the probability that a normally distributed random variable falls within a given interval.

Historical Background

The error function was first studied by mathematicians in the 19th century:

  • Carl Friedrich Gauss (1809): Developed the normal distribution theory
  • James Whitley (1860): Systematic study of the error integral
  • Francis Galton (1890s): Applications in statistics and measurement error
  • Modern era: Algorithmic computation and numerical approximation

Mathematical Properties

The error function possesses numerous important properties:

Analytical Properties
  • Odd function: erf(-x) = -erf(x)
  • Monotonicity: Strictly increasing for all x
  • Boundedness: -1 ≤ erf(x) ≤ 1 for all real x
  • Analyticity: Analytic everywhere in complex plane
Computational Aspects
  • Series expansion: Convergent for all x
  • Continued fractions: Used for efficient computation
  • Approximations: Various polynomial approximations available
  • Numerical stability: Special care needed for large |x|

Connections to Other Special Functions

The error function is related to many other important special functions:

Related Functions
  • Normal distribution CDF: Φ(x) = [1 + erf(x/√2)]/2
  • Gaussian integral: ∫₋∞^∞ e^(-t²) dt = √π
  • Imaginary error: erfi(x) = erf(ix)/i
  • Scaled error: erfcx(x) = e^(x²)·erfc(x)
Integral Forms
  • Laplace transform: ℒ{erf(√t)} = 1/(s√(s+1))
  • Fourier transform: Has known Fourier representation
  • Integration identities: Various integration by parts results
  • Asymptotic behavior: Well-known asymptotic expansions

Applications in Modern Mathematics

Probability & Statistics
  • Normal CDF: Central to normal distribution calculations
  • Confidence limits: Computing confidence intervals
  • Hypothesis testing: Test statistics and p-values
  • Quality control: Process capability indices
Physics & Engineering
  • Heat transfer: Transient conduction problems
  • Diffusion: Mass transfer operations
  • Wave propagation: Gaussian beam propagation
  • Quantum mechanics: Probability distributions
Summary

The error function is one of the most important special functions in applied mathematics. Its close relationship to the normal distribution makes it indispensable for statistical computations. The availability of efficient computational methods and its appearance in numerous applications ensure its continued relevance in scientific and engineering practice.

More statistics functions

Arithmetic Mean • Contraharmonic Mean • Covariance • Empirical distribution CDF • Deviation • Five-Number Summary • Geometric Mean • Harmonic Mean • Inverse Empirical distribution CDF • Kurtosis • Log Geometric Mean • Lower Quartile • Median • Pooled Standard Deviation • Pooled Variance • Skewness (Statistische Schiefe) • Upper Quartile • Variance