Fehlerfunktion erf(x) Rechner

Online Rechner zur Berechnung der Fehlerfunktion erf(x)

Fehlerfunktion Rechner

Die Fehlerfunktion

Die Fehlerfunktion erf(x) ist eine wichtige spezielle Funktion in der Statistik, Wahrscheinlichkeitstheorie und Ingenieurswissenschaften.

Parameter eingeben

Argument x

Argument x eingeben (üblicherweise -5 bis 5)

Dezimalstellen

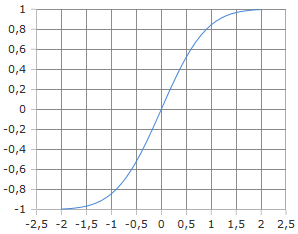
Fehlerfunktion Ergebnis

erf(x):

Fehlerfunktionswert

Fehlerfunktion Eigenschaften

Bereich: -1 ≤ erf(x) ≤ 1, Ungerade Funktion mit erf(0) = 0

-1 ≤ erf(x) ≤ 1 Ungerade Funktion erf(0) = 0

Fehlerfunktion Kurve

Die Fehlerfunktion hat ein sigmoidales Verhalten.
Schneller Übergang von -1 zu +1 um x = 0.

Was ist die Fehlerfunktion?

Die Fehlerfunktion erf(x) ist eine fundamentale mathematische Funktion:

Definition: erf(x) = (2/√π) ∫₀ˣ e^(-t²) dt
Bereich: -1 ≤ erf(x) ≤ 1
Ungerade Funktion: erf(-x) = -erf(x)

Anwendung: Statistik, Wahrscheinlichkeit, Wärmeübertragung, Quantenmechanik
Verwandt mit: Normalverteilung, komplementäre Fehlerfunktion erfc(x)
Eigenschaften: Glatt, monoton steigend, differenzierbar

Eigenschaften und Beziehungen

Die Fehlerfunktion hat wichtige mathematische Eigenschaften:

Schlüsseleigenschaften

Ungerade Symmetrie: erf(-x) = -erf(x)
Randwerte: erf(0) = 0, erf(∞) = 1
Ableitung: d/dx[erf(x)] = (2/√π)e^(-x²)
Taylorreihe: erf(x) = (2/√π)Σ(-1)ⁿx^(2n+1)/(n!(2n+1))

Anwendungen der Fehlerfunktion

Die Fehlerfunktion wird in vielen wissenschaftlichen und ingenieurswissenschaftlichen Bereichen verwendet:

Statistik & Wahrscheinlichkeit

Normalverteilung CDF-Berechnung
Konfidenzintervalle
Statistische Hypothesentests
Wahrscheinlichkeitsdichte-Berechnungen

Physik & Ingenieurswesen

Wärmediffusionsgleichungen
Diffusionsprozesse
Quantenmechanische Wellenfunktionen
Signalverarbeitungsfilter

Wissenschaft & Messtechnik

Fehleranalyse in Messungen
Unsicherheitsquantifizierung
Kalibrierungskurven
Instrumentelle Präzision

Numerische Methoden

Näherungsalgorithmen
Reihenentwicklungen
Kettenbrüche
Berechnungseffizienz

Formeln für die Fehlerfunktion

Fehlerfunktion (Integraldefinition)

\[erf(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} dt\]

Standard-Integraldefinition mit Gaußscher Form

Komplementäre Fehlerfunktion

\[erfc(x) = 1 - erf(x) = \frac{2}{\sqrt{\pi}} \int_x^{\infty} e^{-t^2} dt\]

Tail-Wahrscheinlichkeit der Normalverteilung

Taylorreihe

\[erf(x) = \frac{2}{\sqrt{\pi}} \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{n!(2n+1)}\]

Potenzreihenentwicklung um x = 0

Ableitung

\[\frac{d}{dx}erf(x) = \frac{2}{\sqrt{\pi}} e^{-x^2}\]

Ableitung ist eine Gaußsche Funktion

Inverse Fehlerfunktion

\[x = erf^{-1}(y), \quad -1 < y < 1\]

Umkehrfunktion zum Finden des Arguments aus dem Wert

Asymptotische Entwicklung (große x)

\[erf(x) \approx 1 - \frac{e^{-x^2}}{\sqrt{\pi}x} \quad \text{für große } x\]

Näherung für große Argumentwerte

Beispielrechnungen für die Fehlerfunktion

Beispiel 1: Normalverteilung CDF

Standardnormalverteilung, P(Z ≤ 1)

Beziehung zur Normalverteilung

Standardnormalverteilung: N(0,1)
Gesucht: P(Z ≤ 1)
Beziehung: P(Z ≤ x) = [1 + erf(x/√2)]/2

Berechnung: P(Z ≤ 1) = [1 + erf(1/√2)]/2

Lösung

\[erf(1/\sqrt{2}) = erf(0.7071) \approx 0.6827\] \[P(Z \leq 1) = \frac{1 + 0.6827}{2} = 0.8414\] \[= 84.14\%\]

Interpretation: Etwa 84.14% einer Standardnormalverteilung liegt unter einer Standardabweichung über dem Mittelwert.

Beispiel 2: Wärmediffusion

Halbunendliches Medium, x = 0.5, α·t/L² = 0.5

Physikalisches Problem

Wärmediffusion in halbunendlichem Medium
Temperaturprofil in Tiefe x
Lösung beinhaltet komplementäre Fehlerfunktion

Formel: T = T₀ + (T₁ - T₀)erfc(η)

Berechnung

\[\eta = \frac{x}{2\sqrt{\alpha t}} = 0.5\] \[erfc(0.5) = 1 - erf(0.5)\] \[= 1 - 0.5205 = 0.4795\]

Anwendung: Die Fehlerfunktion löst transiente Wärmeleitung.

Beispiel 3: Rechner Standardwert

x = 0.5

Direkte Berechnung

\[erf(0.5) = \frac{2}{\sqrt{\pi}} \int_0^{0.5} e^{-t^2} dt\] \[\approx 0.5205\]

Fehlerfunktion Werte

x	erf(x)	erfc(x)	Ungefähr %-Perzentil
0.0	0.0000	1.0000	50.00%
0.5	0.5205	0.4795	69.85%
1.0	0.8427	0.1573	84.27%
1.5	0.9661	0.0339	93.31%
2.0	0.9953	0.0047	97.73%
2.5	0.9999	0.0001	99.38%

Mathematische Grundlagen der Fehlerfunktion

Die Fehlerfunktion ist eine fundamentale spezielle Funktion in der Mathematik, die natürlich in der Wahrscheinlichkeitstheorie, Statistik und der Lösung von Differentialgleichungen auftritt. Sie repräsentiert die Wahrscheinlichkeit, dass eine normalverteilte Zufallsvariable in ein gegebenes Intervall fällt.

Historischer Hintergrund

Die Fehlerfunktion wurde erstmals von Mathematikern im 19. Jahrhundert studiert:

Carl Friedrich Gauss (1809): Entwicklung der Normalverteilungstheorie
James Whitley (1860): Systematische Studie des Fehlerintegrals
Francis Galton (1890er): Anwendungen in Statistik und Messfehler
Moderne Ära: Algorithmische Berechnung und numerische Näherung

Mathematische Eigenschaften

Die Fehlerfunktion besitzt zahlreiche wichtige Eigenschaften:

Analytische Eigenschaften

Ungerade Funktion: erf(-x) = -erf(x)
Monotonie: Streng monoton steigend für alle x
Beschränktheit: -1 ≤ erf(x) ≤ 1 für alle reellen x
Analytizität: Analytisch überall in der komplexen Ebene

Berechnungsaspekte

Reihenentwicklung: Konvergent für alle x
Kettenbrüche: Verwendet für effiziente Berechnung
Näherungen: Verschiedene Polynomialnäherungen verfügbar
Numerische Stabilität: Besondere Vorsicht für große |x| erforderlich

Zusammenfassung

Die Fehlerfunktion ist eine der wichtigsten speziellen Funktionen in der angewandten Mathematik. Ihre enge Beziehung zur Normalverteilung macht sie unverzichtbar für statistische Berechnungen. Die Verfügbarkeit effizienter Berechnungsmethoden und ihr Auftreten in zahlreichen Anwendungen gewährleisten ihre anhaltende Relevanz in wissenschaftlicher und ingenieurtechnischer Praxis.