Complementary Error Function Calculator
Online calculator for computing the complementary error function erfc(x)
Complementary Error Function Calculator
The Complementary Error Function
The complementary error function erfc(x) represents the tail probability of the normal distribution and is essential for statistical inference and probability calculations.
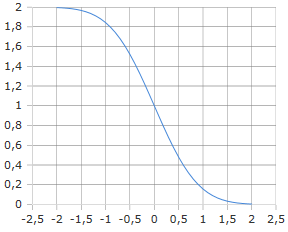
Complementary Error Function Curve
The erfc(x) function decays from 2 to 0 as x increases.
It represents tail probability of the normal distribution.
|
|
What is the Complementary Error Function?
The complementary error function erfc(x) is the complement of the error function:
- Definition: erfc(x) = 1 - erf(x) = (2/√π) ∫ₓ^∞ e^(-t²) dt
- Range: 0 ≤ erfc(x) ≤ 2
- Even/Odd: Symmetric around x = 0 for erf transformation
- Application: Tail probabilities, normal distribution CDF
- Related to: Error function erf(x), Q-function
- Properties: Smooth, monotonically decreasing
Tail Probabilities and Statistical Applications
The complementary error function is fundamental for computing tail probabilities:
Normal Distribution Tail
- Relationship: P(X > x) = (1/2)erfc(x/√2) for standard normal
- Upper tail: Probability in the right tail
- p-values: Connection to statistical significance
- Critical values: Thresholds for hypothesis tests
Quantile Functions
- Inverse erfc: Computing critical values
- Confidence limits: Confidence interval boundaries
- Survival analysis: Reliability and survival curves
- Risk quantification: Value-at-Risk calculations
Applications of the Complementary Error Function
The complementary error function is used extensively in statistics and engineering:
Statistics & Probability
- Normal distribution tail probabilities
- Confidence interval calculation
- Hypothesis test p-values
- Quality control and process capability
Physics & Engineering
- Heat diffusion and thermal analysis
- Signal detection and noise analysis
- Reliability engineering
- Diffusion processes
Finance & Risk
- Value-at-Risk (VaR) calculations
- Portfolio risk assessment
- Expected shortfall computations
- Option pricing in financial markets
Communication Theory
- Bit error rate (BER) analysis
- Signal detection theory
- Channel capacity calculations
- Receiver operating characteristic (ROC) curves
Formulas for the Complementary Error Function
Complementary Error Function (Integral)
Tail integral of Gaussian function
Relationship to Error Function
Complementary property with erf(x)
Normal Distribution Connection
Standard normal tail probability
Taylor Series
Series expansion for small x
Asymptotic Expansion (Large x)
Approximation for large argument values
Derivative
Negative of Gaussian function
Example Calculations for the Complementary Error Function
Example 1: Normal Distribution Tail Probability
Question
- Standard normal: N(0,1)
- Find: Probability that Z > 1
- Relationship: P(Z > 1) = (1/2)erfc(1/√2)
Solution
Example 2: Quality Control - Defect Rate
Problem Setup
- Product dimension: nominal 100 mm
- Specification: 98-102 mm
- Process: μ = 100, σ = 0.8 mm
Calculation
Example 3: Calculator Default Value
Direct Calculation
Related Values
Complementary Error Function Values
| x | erfc(x) | erf(x) | Normal Tail % |
|---|---|---|---|
| 0.0 | 1.0000 | 0.0000 | 50.00% |
| 0.5 | 0.4795 | 0.5205 | 30.15% |
| 1.0 | 0.1573 | 0.8427 | 15.73% |
| 1.5 | 0.0339 | 0.9661 | 6.68% |
| 2.0 | 0.0047 | 0.9953 | 2.27% |
| 2.5 | 0.0001 | 0.9999 | 0.62% |
Mathematical Foundations of the Complementary Error Function
The complementary error function erfc(x) is the natural representation of tail probabilities in normal distribution calculations. It appears naturally in the solution of many differential equations and is fundamental to probability theory and statistical inference.
Historical Development
The error function and its complement were developed in the 19th century:
- Carl Friedrich Gauss (1809): Foundation of normal distribution theory
- James Whitley (1860): Systematic tabulation of error integrals
- James Whitworth (1890s): Engineering applications in quality control
- Modern era: Numerical algorithms and computational methods
Mathematical Properties
The complementary error function has important analytical properties:
Analytical Properties
- Bounds: 0 ≤ erfc(x) ≤ 2 for all real x
- Monotonicity: Strictly decreasing function
- Limits: lim_{x→-∞} erfc(x) = 2, lim_{x→∞} erfc(x) = 0
- Symmetry: erfc(-x) = 2 - erfc(x)
Computational Aspects
- Series: Different series for different x ranges
- Continued fractions: Used for efficient computation
- Asymptotic: Well-approximated for large |x|
- Stability: Numerical stability considerations for extreme values
Connections to Other Functions
The complementary error function is related to many important mathematical functions:
Statistical Functions
- Q-function: Q(x) = (1/2)erfc(x/√2) = P(Z > x) for standard normal
- Standard normal CDF: Φ(x) = 1 - (1/2)erfc(x/√2)
- t-distribution: Tail probabilities derived via erfc
- Chi-square: Connection through gamma function
Special Functions
- Gaussian: exp(-x²) appears in both erf and erfc
- Dawson's integral: Related through similarity transformation
- Parabolic cylinder functions: Connection via differential equations
- Hypergeometric: Expressible via hypergeometric functions
Applications in Modern Sciences
Physics & Engineering
- Heat diffusion and thermal conduction
- Signal detection in communication systems
- Reliability and life testing analysis
- Quantum mechanical wave packets
Finance & Risk Management
- Value-at-Risk (VaR) calculations
- Option pricing models
- Credit risk assessment
- Portfolio optimization
Summary
The complementary error function is an indispensable tool in applied mathematics and statistics. Its role in representing tail probabilities makes it essential for probability calculations, quality control, risk assessment, and hypothesis testing. The availability of efficient computational algorithms and its presence in modern scientific software ensure its continued relevance in research, engineering, and data analysis.
|
|
|
|