Komplementäre Fehlerfunktion erfc(x) Rechner

Online Rechner zur Berechnung der komplementären Fehlerfunktion erfc(x)

Komplementäre Fehlerfunktion Rechner

Die Komplementäre Fehlerfunktion

Die komplementäre Fehlerfunktion erfc(x) repräsentiert die Tail-Wahrscheinlichkeit der Normalverteilung und ist von grundlegender Bedeutung für statistische Inferenz und Wahrscheinlichkeitsrechnungen.

Parameter eingeben
Argument x eingeben (üblicherweise -5 bis 5)
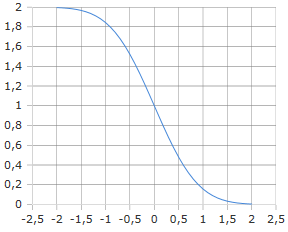
Komplementäre Fehlerfunktion Ergebnis
erfc(x):
Komplementäre Fehlerfunktionswert (Tail-Wahrscheinlichkeit)
Komplementäre Fehlerfunktion Eigenschaften

Beziehung: erfc(x) = 1 - erf(x), Bereich: 0 ≤ erfc(x) ≤ 2

0 ≤ erfc(x) ≤ 2 erfc(0) = 1 Tail-Wahrscheinlichkeit

Komplementäre Fehlerfunktion Kurve

Die erfc(x) Funktion fällt von 2 auf 0 mit steigendem x.
Sie repräsentiert die Tail-Wahrscheinlichkeit der Normalverteilung.

Komplementäre Fehlerfunktion


Was ist die Komplementäre Fehlerfunktion?

Die komplementäre Fehlerfunktion erfc(x) ist das Komplement zur Fehlerfunktion:

  • Definition: erfc(x) = 1 - erf(x) = (2/√π) ∫ₓ^∞ e^(-t²) dt
  • Bereich: 0 ≤ erfc(x) ≤ 2
  • Symmetrie: Symmetrisch bezüglich erf-Transformation
  • Anwendung: Tail-Wahrscheinlichkeiten, Normalverteilung CDF
  • Verwandt mit: Fehlerfunktion erf(x), Q-Funktion
  • Eigenschaften: Glatt, monoton fallend

Tail-Wahrscheinlichkeiten und statistische Anwendungen

Die komplementäre Fehlerfunktion ist fundamental für die Berechnung von Tail-Wahrscheinlichkeiten:

Normalverteilung Tail
  • Beziehung: P(X > x) = (1/2)erfc(x/√2) für Standardnormal
  • Oberer Tail: Wahrscheinlichkeit im rechten Schwanz
  • p-Werte: Verbindung zur statistischen Signifikanz
  • Kritische Werte: Schwellenwerte für Hypothesentests
Quantilfunktionen
  • Inverse erfc: Berechnung kritischer Werte
  • Konfidenzgrenzen: Konfidenzintervallgrenzen
  • Überlebensanalyse: Zuverlässigkeits- und Überlebenskurven
  • Risikoquantifizierung: Value-at-Risk Berechnungen

Anwendungen der Komplementären Fehlerfunktion

Die komplementäre Fehlerfunktion wird umfassend in Statistik und Ingenieurswesen verwendet:

Statistik & Wahrscheinlichkeit
  • Normalverteilung Tail-Wahrscheinlichkeiten
  • Konfidenzintervall-Berechnung
  • Hypothesentest p-Werte
  • Qualitätskontrolle und Prozesstauglichkeit
Physik & Ingenieurswesen
  • Wärmediffusion und thermische Analyse
  • Signaldetektion und Rauschanalyse
  • Zuverlässigkeitstechnik
  • Diffusionsprozesse
Finanzwesen & Risiko
  • Value-at-Risk (VaR) Berechnungen
  • Portfolio-Risikobewertung
  • Expected Shortfall Berechnungen
  • Optionspreismodelle in Finanzmärkten
Kommunikationstheorie
  • Bitfehlerrate (BER) Analyse
  • Signaldetektionstheorie
  • Kanalkapazitätsberechnungen
  • Receiver Operating Characteristic (ROC) Kurven

Formeln für die Komplementäre Fehlerfunktion

Komplementäre Fehlerfunktion (Integral)
\[erfc(x) = \frac{2}{\sqrt{\pi}} \int_x^{\infty} e^{-t^2} dt\]

Tail-Integral der Gaußschen Funktion

Beziehung zur Fehlerfunktion
\[erfc(x) = 1 - erf(x)\]

Komplementäre Eigenschaft mit erf(x)

Normalverteilung Verbindung
\[P(X > x) = \frac{1}{2}erfc\left(\frac{x}{\sqrt{2}}\right) \quad \text{für } X \sim N(0,1)\]

Standardnormal Tail-Wahrscheinlichkeit

Taylorreihe
\[erfc(x) = 1 - \frac{2}{\sqrt{\pi}} \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{n!(2n+1)}\]

Reihenentwicklung für kleine x

Asymptotische Entwicklung (Große x)
\[erfc(x) \approx \frac{e^{-x^2}}{\sqrt{\pi}x} \quad \text{für große } x\]

Näherung für große Argumentwerte

Ableitung
\[\frac{d}{dx}erfc(x) = -\frac{2}{\sqrt{\pi}} e^{-x^2}\]

Negative der Gaußschen Funktion

Beispielrechnungen für die Komplementäre Fehlerfunktion

Beispiel 1: Normalverteilung Tail-Wahrscheinlichkeit
Standardnormal, P(Z > 1)
Aufgabe
  • Standardnormalverteilung: N(0,1)
  • Gesucht: Wahrscheinlichkeit dass Z > 1
  • Beziehung: P(Z > 1) = (1/2)erfc(1/√2)
Berechnung: P(Z > 1) = (1/2)erfc(0.7071)
Lösung
\[erfc(0.7071) \approx 0.3173\] \[P(Z > 1) = \frac{1}{2} \times 0.3173 = 0.1587\] \[= 15.87\%\]
Interpretation: Etwa 15.87% einer Standardnormalverteilung liegt über einer Standardabweichung.
Beispiel 2: Qualitätskontrolle - Ausschussrate
Produktspezifikationsgrenzen, Ausschusswahrscheinlichkeit
Problemstellung
  • Produktabmessung: Nennmaß 100 mm
  • Spezifikation: 98-102 mm
  • Prozess: μ = 100, σ = 0.8 mm
Gesucht: P(X > 102)
Berechnung
\[Z = \frac{102 - 100}{0.8} = 2.5\] \[P(X > 102) = \frac{1}{2}erfc\left(\frac{2.5}{\sqrt{2}}\right)\] \[= \frac{1}{2}erfc(1.768) \approx 0.0038\] \[= 0.38\% \text{ Ausschussrate}\]
Anwendung: Die komplementäre Fehlerfunktion berechnet Ausschussraten in der Fertigung.
Beispiel 3: Rechner Standardwert
x = 0.5
Direkte Berechnung
\[erfc(0.5) = \frac{2}{\sqrt{\pi}} \int_{0.5}^{\infty} e^{-t^2} dt\] \[\approx 0.4795\]
Verwandte Werte
\[erf(0.5) \approx 0.5205\] \[erf(0.5) + erfc(0.5) = 1\] \[0.5205 + 0.4795 = 1.0000\]
Komplementäre Fehlerfunktion Werte
x erfc(x) erf(x) Normal Tail %
0.01.00000.000050.00%
0.50.47950.520530.15%
1.00.15730.842715.73%
1.50.03390.96616.68%
2.00.00470.99532.27%
2.50.00010.99990.62%

Mathematische Grundlagen der Komplementären Fehlerfunktion

Die komplementäre Fehlerfunktion erfc(x) ist die natürliche Darstellung von Tail-Wahrscheinlichkeiten in Normalverteilungsberechnungen. Sie tritt natürlich in der Lösung vieler Differentialgleichungen auf und ist fundamental für Wahrscheinlichkeitstheorie und statistische Inferenz.

Historische Entwicklung

Die Fehlerfunktion und ihr Komplement wurden im 19. Jahrhundert entwickelt:

  • Carl Friedrich Gauss (1809): Grundlagen der Normalverteilungstheorie
  • James Whitley (1860): Systematische Tabellierung von Fehlerintegralen
  • James Whitworth (1890er): Ingenieursanwendungen in der Qualitätskontrolle
  • Moderne Ära: Numerische Algorithmen und Berechnungsmethoden

Mathematische Eigenschaften

Die komplementäre Fehlerfunktion hat wichtige analytische Eigenschaften:

Analytische Eigenschaften
  • Grenzen: 0 ≤ erfc(x) ≤ 2 für alle reellen x
  • Monotonie: Streng monoton fallende Funktion
  • Grenzwerte: lim_{x→-∞} erfc(x) = 2, lim_{x→∞} erfc(x) = 0
  • Symmetrie: erfc(-x) = 2 - erfc(x)
Berechnungsaspekte
  • Reihen: Verschiedene Reihen für verschiedene x-Bereiche
  • Kettenbrüche: Verwendet für effiziente Berechnung
  • Asymptotisch: Gut approximiert für große |x|
  • Stabilität: Numerische Stabilitätsüberlegungen für Extremwerte

Verbindungen zu anderen Funktionen

Die komplementäre Fehlerfunktion ist mit vielen wichtigen mathematischen Funktionen verwandt:

Statistische Funktionen
  • Q-Funktion: Q(x) = (1/2)erfc(x/√2) = P(Z > x) für Standardnormal
  • Standard Normal CDF: Φ(x) = 1 - (1/2)erfc(x/√2)
  • t-Verteilung: Tail-Wahrscheinlichkeiten über erfc hergeleitet
  • Chi-Quadrat: Verbindung über Gamma-Funktion
Spezielle Funktionen
  • Gaußsche: exp(-x²) erscheint in sowohl erf als auch erfc
  • Dawson-Integral: Verwandt durch Ähnlichkeitstransformation
  • Parabolische Zylinderfunktionen: Verbindung über Differentialgleichungen
  • Hypergeometrische: Darstellbar über hypergeometrische Funktionen

Anwendungen in modernen Wissenschaften

Physik & Ingenieurswesen
  • Wärmediffusion und thermische Leitung
  • Signaldetektion in Kommunikationssystemen
  • Zuverlässigkeits- und Lebensdaueranalyse
  • Quantenmechanische Wellenpakete
Finanzwesen & Risikomanagement
  • Value-at-Risk (VaR) Berechnungen
  • Optionspreismodelle
  • Kreditrisikobewertung
  • Portfoliooptimierung
Zusammenfassung

Die komplementäre Fehlerfunktion ist ein unverzichtbares Werkzeug in der angewandten Mathematik und Statistik. Ihre Rolle bei der Darstellung von Tail-Wahrscheinlichkeiten macht sie wesentlich für Wahrscheinlichkeitsberechnungen, Qualitätskontrolle, Risikobewertung und Hypothesentests. Die Verfügbarkeit effizienter Berechnungsalgorithmen und ihre Präsenz in moderner wissenschaftlicher Software gewährleisten ihre anhaltende Relevanz in Forschung, Technik und Datenanalyse.

Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?

Wahrscheinlichkeiten

Geburtstagsparadoxon • Satz von Bayes • Zentraler Grenzwertsatz

Statistik Funktionen

Arithmetisches Mittel (Durchschnitt) • Empirische Inverse Verteilungsfunktion • Empirische Verteilungsfunktion • Five-Number Summary • Empirische inverse Verteilungsfunktion CDF • Geometrisches Mittel • Gepoolte Standardabweichung • Gepoolte Varianz • Harmonisches Mittel • Kontraharmonisches Mittel • Kovarianz • Kurtosis (Wölbung) • Log-Geometrisches Mittel • Median • Modus • Oberes Quartil • Skewness (Statistische Schiefe) • Standardabweichung • Unteres Quartil • Varianz

Statistik Distanz Funktionen

Dice Index • Hellingerabstand • Jaccard Index • Mittlerer Absoluter Fehler • Mittlerer Quadratischer Fehler • Summe der Absoluten Differenz • Summe der Abweichungsquadrate

Kombinatorik Funktionen

Kombinationen ohne Wiederholung • Kombinationen mit Wiederholung • Permutationen ohne Wiederholung • Produktregel • Variationen ohne Wiederholung • Variationen mit Wiederholung • Aktivitäten Auswahl Problem