Inverse Error Function Calculator
Online calculator for computing the inverse error function erfi(x)
Inverse Error Function Calculator
The Inverse Error Function
The inverse error function erfi(x) computes quantiles of the normal distribution and is essential for statistical inference and critical values.
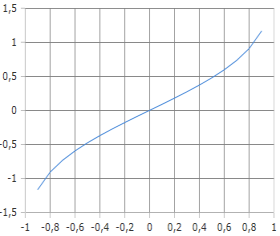
Inverse Error Function Curve
The curve shows the inverse mapping from probability to argument.
Strictly increasing function with symmetric behavior.
|
|
What is the Inverse Error Function?
The inverse error function erfi(x) is the inverse of the error function:
- Definition: erfi(y) is the x such that erf(x) = y
- Quantile Function: Computes standard normal quantiles
- Range: -1 ≤ y ≤ 1
- Application: Statistical hypothesis tests, confidence intervals, normal quantiles
- Significance: Bridge between probability and z-values
- Related to: Normal distribution quantiles, probit function
Normal Quantiles and Statistical Applications
The inverse error function is fundamental for normal distribution calculations:
Normal Quantile Interpretation
- z-Score: erfi(p) = √2 × Φ⁻¹((p+1)/2)
- Percentiles: Converting probabilities to z-values
- Critical Values: Statistical test thresholds
- Confidence Limits: Interval boundary calculations
Probit Analysis
- Probit Function: Link function in regression
- Dose-Response: Biological assay analysis
- Binary Outcomes: Logistic regression alternative
- Threshold Models: Latent variable modeling
Applications of the Inverse Error Function
The inverse error function is essential for statistics and scientific computing:
Statistical Inference
- Normal distribution quantiles
- Critical values for z-tests
- Confidence interval computation
- p-value transformations
Biometric Analysis
- Probit regression modeling
- Dose-response curves
- LD50 and EC50 calculations
- Tolerance distribution analysis
Monte Carlo Simulation
- Normal random number generation
- Box-Muller transformation
- Gaussian process simulation
- Stochastic modeling
Engineering Applications
- Quality control specifications
- Reliability engineering
- Optimization algorithms
- Signal processing filters
Formulas for the Inverse Error Function
Inverse Function Definition
x is the argument such that the error function yields y
Normal Quantile Relationship
Connection to standard normal quantile function Φ⁻¹
Probit Function Connection
Link to probit function for probability p
Inverse Relationship
Fundamental identity for inverse functions
Series Expansion (Small y)
Taylor series for small argument values
Symmetry Property
Odd function property
Example Calculations for the Inverse Error Function
Example 1: Standard Normal Quantile
Question
- Standard normal distribution: N(0,1)
- Find: 95th percentile (z₀.₀₅)
- Probability: 95% = 0.95
Calculation
Example 2: Probit Analysis (Dose-Response)
Problem
- Dose-response study: toxicity assessment
- Find: probit value for 50% response
- Response probability: p = 0.5
Solution
Example 3: Calculator Default Value
Question
Calculation Result
Inverse Error Function Values
| y (erf value) | erfi(y) | Normal Percentile | Statistical Use |
|---|---|---|---|
| 0.0 | 0.0000 | 50th percentile | Median |
| 0.3 | 0.2724 | 65th percentile | Mild significance |
| 0.6 | 0.5951 | 80th percentile | Moderate significance |
| 0.9 | 1.1631 | 95th percentile | High significance |
| 0.95 | 1.3859 | 97.5th percentile | Very high significance |
| 0.99 | 1.8214 | 99.5th percentile | Extreme significance |
Mathematical Foundations of the Inverse Error Function
The inverse error function erfi(x) is the inverse of the error function and provides the mathematical foundation for computing normal distribution quantiles. It is essential for statistical inference, hypothesis testing, and confidence interval construction.
Historical Development
The development of the inverse error function paralleled advances in probability theory:
- Carl Friedrich Gauss (1809): Normal distribution theory foundation
- Pierre-Simon Laplace (1812): Central limit theorem and normal approximations
- Francis Galton (1880s): Practical applications in biometry
- Ronald Fisher (1920s): Statistical inference and hypothesis testing
- Modern era: Numerical algorithms and computational implementations
Mathematical Properties
The inverse error function has important analytical properties:
Analytical Properties
- Odd function: erfi(-y) = -erfi(y)
- Monotonicity: Strictly increasing
- Domain: -1 ≤ y ≤ 1
- Range: -∞ < erfi(y) < +∞
Computational Aspects
- Series expansion: For small arguments
- Asymptotic expansion: For large arguments
- Rational approximations: For efficient computation
- Newton-Raphson: Iterative root finding
Connections to Other Functions
The inverse error function is related to many important statistical functions:
Statistical Functions
- Normal quantile: Φ⁻¹(p) = √2 × erfi(2p-1)
- Probit function: probit(p) = √2 × erfi(2p-1)
- z-scores: Critical values for hypothesis tests
- Confidence limits: Interval boundary calculations
Special Functions
- Dawson integral: Related special function
- Fresnel integrals: Connection via complex analysis
- Gamma function: Probabilistic representation
- Hypergeometric functions: Series representations
Applications in Modern Sciences
Statistics & Inference
- Hypothesis test critical values
- Confidence interval boundaries
- p-value computations
- Sample size determinations
Applied Sciences
- Quality control and Six Sigma
- Biostatistics and clinical trials
- Econometrics and finance
- Engineering reliability analysis
Summary
The inverse error function is a cornerstone of statistical computing and data analysis. Its role in converting probabilities to standard normal quantiles makes it indispensable for hypothesis testing, confidence intervals, and statistical modeling. From quality control in manufacturing to clinical trial analysis in medicine, it provides the mathematical foundation for evidence-based decision making.
|
|
|
|