Inverse Fehlerfunktion erfi(x) berechnen

Online Rechner und Formel zur Berechnung der inversen Fehlerfunktion erfi(x)

erfi(x) Rechner

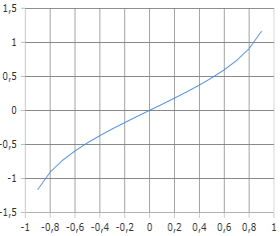
Inverse Fehlerfunktion

Der Rechner berechnet die inverse Fehlerfunktion erfi(x), die Umkehrfunktion von erf(x) mit der Eigenschaft erfi(erf(y)) = y.

Wert zwischen -1 und 1 für die inverse Fehlerfunktion
Resultat
erfi(x):

Inverse Fehlerfunktion Kurve


Erfi Funktion

Grafische Darstellung der inversen Fehlerfunktion erfi(x) mit charakteristischem monoton steigenden Verlauf.

Formeln zur erfi(x) Funktion

Inverse Fehlerfunktion
\[\displaystyle erfi(x) = erf^{-1}(x)\]
Inverse Eigenschaft
\[\displaystyle erf^{-1}(erf(x)) = x\]
Definitionsbereich
\[-1 < x < 1\]
Fehlerfunktion
\[\displaystyle erf(x)= \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2}dt\]
Komplementärbeziehung
\[\displaystyle erf(x)+erfc(x)=1\]
Spezialwerte
\[erfi(0) = 0\] \[erfi(1) = +\infty\] \[erfi(-1) = -\infty\]

Beschreibung der inversen Fehlerfunktion

Mathematische Definition

Der Rechner auf dieser Seite berechnet die inverse Fehlerfunktion erfi(x). Diese Funktion ist die Umkehrfunktion der Fehlerfunktion erf(x) und wird zur Bestimmung von Quantilen der Normalverteilung verwendet.

Hinweise zur Berechnung

Zur Berechnung geben Sie das Argument x ein. Dann klicken Sie den Button 'Rechnen'. Das Argument muss im Bereich -1 < x < 1 liegen.

Eigenschaften und Anwendungen

Umkehrfunktion

Die inverse Fehlerfunktion ist die Umkehrfunktion von erf(x): erfi(erf(y)) = y

Definitionsbereich
  • Eingabe: -1 < x < 1
  • erfi(0) = 0
  • erfi(1) = +∞ (Grenzwert)
  • erfi(-1) = -∞ (Grenzwert)
Anwendungsbereiche

Quantilberechnung der Normalverteilung, Monte-Carlo-Simulationen, Zufallszahlengenerierung und statistische Inferenz.


Wahrscheinlichkeiten

Geburtstagsparadoxon • Satz von Bayes • Zentraler Grenzwertsatz

Statistik Funktionen

Arithmetisches Mittel (Durchschnitt) • Empirische Inverse Verteilungsfunktion • Empirische Verteilungsfunktion • Five-Number Summary • Empirische inverse Verteilungsfunktion CDF • Geometrisches Mittel • Gepoolte Standardabweichung • Gepoolte Varianz • Harmonisches Mittel • Kontraharmonisches Mittel • Kovarianz • Kurtosis (Wölbung) • Log-Geometrisches Mittel • Median • Modus • Oberes Quartil • Skewness (Statistische Schiefe) • Standardabweichung • Unteres Quartil • Varianz

Statistik Distanz Funktionen

Dice Index • Hellingerabstand • Jaccard Index • Mittlerer Absoluter Fehler • Mittlerer Quadratischer Fehler • Summe der Absoluten Differenz • Summe der Abweichungsquadrate

Kombinatorik Funktionen

Kombinationen ohne Wiederholung • Kombinationen mit Wiederholung • Permutationen ohne Wiederholung • Produktregel • Variationen ohne Wiederholung • Variationen mit Wiederholung • Aktivitäten Auswahl Problem