Set Complement

Calculator for computing set complements with comprehensive formulas and examples

Set Complement Calculator

What is calculated?

The complement of set A with respect to a universal set U contains all elements of U that are not in A. Notation: Ac or Ā or U \ A.

Enter the Sets

Elements of subset A

All possible elements (must contain A)
Result (Ac)
Complement:
All elements of the universal set that are not in A

Complement Info

Properties

Complement Ac:

  • Ac = U \ A (Difference to universal set)
  • A ∪ Ac = U (Union equals U)
  • A ∩ Ac = ∅ (Intersection is empty)
  • (Ac)c = A (Double complement)
Complement Venn Diagram

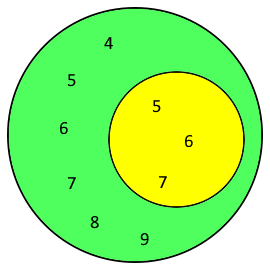
Venn diagram of the complement

Memory aid: "The complement of A contains all elements of the universal set that are not in A."

Examples
Standard:
U = {1,2,3,4,5}, A = {1,3}
Ac = {2,4,5}
Empty set:
∅c = U
Universal set:
Uc = ∅
Related Operations

→ Set Difference
→ Set Union
→ Set Intersection


Complement Formulas

Basic Definition
\[A^c = \{x : x \in U \land x \notin A\}\] Set notation
Set Difference
\[A^c = U \setminus A\] As set difference
De Morgan 1
\[(A \cup B)^c = A^c \cap B^c\] Complement of union
De Morgan 2
\[(A \cap B)^c = A^c \cup B^c\] Complement of intersection
Double Complement
\[(A^c)^c = A\] Involution
Complement Laws
\[A \cup A^c = U\] \[A \cap A^c = \emptyset\] Basic laws

Detailed Calculation Example

Example: A = {5,6,7}, U = {4,5,6,7,8,9}

Given:

  • A = {5, 6, 7} (Subset)
  • U = {4, 5, 6, 7, 8, 9} (Universal set)

Step 1 - Verification:

A ⊆ U ? {5,6,7} ⊆ {4,5,6,7,8,9} ✓
All elements of A are contained in U

Step 2 - Determine complement:

4 ∈ U and 4 ∉ A ✓
5 ∈ U and 5 ∈ A ✗
6 ∈ U and 6 ∈ A ✗
7 ∈ U and 7 ∈ A ✗
8 ∈ U and 8 ∉ A ✓
9 ∈ U and 9 ∉ A ✓

Step 3 - Result:

Ac = {4, 8, 9}

Interpretation: The complement of A with respect to U contains the elements 4, 8, 9, which are in the universal set but not in A.

Practical Application Example

Example: Students in a class and elective courses

All students in the class (U):

Anna, Ben, Clara, David, Eva, Franz, Greta, Hans, Ina, Jörg

French course participants (A):

Clara, David, Eva, Hans

Question: Which students are NOT taking the French course?

Answer (Ac): Anna, Ben, Franz, Greta, Ina, Jörg

Result: 6 out of 10 students are not taking the French course.

De Morgan's Laws

The fundamental laws of set theory
First Law
\[(A \cup B)^c = A^c \cap B^c\]

The complement of the union is the intersection of the complements

Second Law
\[(A \cap B)^c = A^c \cup B^c\]

The complement of the intersection is the union of the complements

Practical Example

Given: U = {1,2,3,4,5,6}, A = {1,2,3}, B = {3,4,5}

Check first law:
A ∪ B = {1,2,3,4,5}
(A ∪ B)c = {6}

Ac = {4,5,6}, Bc = {1,2,6}
Ac ∩ Bc = {6} ✓
Check second law:
A ∩ B = {3}
(A ∩ B)c = {1,2,4,5,6}

Ac ∪ Bc = {1,2,4,5,6} ✓

Mathematical Properties

Basic Properties
  • Involution: (Ac)c = A
  • Complementarity: A ∪ Ac = U
  • Disjointness: A ∩ Ac = ∅
  • Uniqueness: Ac is uniquely determined
Special Cases
  • Empty set: ∅c = U
  • Universal set: Uc = ∅
  • Subsets: If A ⊆ B, then Bc ⊆ Ac
  • Cardinality: |Ac| = |U| - |A|
Important Notes

Consider universal set: The complement is always relative to the chosen universal set

Subset property: A must be a subset of U

Practical Applications

Computer Science
  • Boolean algebra
  • Logical operations
  • Database queries (NOT)
  • Bit manipulation
Statistics
  • Complementary events
  • Probability theory
  • Opposite events
  • Exclusion methods
Administration
  • Exclusion lists
  • Identify non-participants
  • Find missing elements
  • Categorization




Set theory functions

Complement  •  Difference  •  Intersection  •  Symmetric Difference  •  Union  •