Komplement einer Menge

Rechner zur Berechnung des Komplements einer Menge mit ausführlichen Formeln und Beispielen

Komplement Rechner

Was wird berechnet?

Das Komplement einer Menge A bezüglich einer Universalmenge U enthält alle Elemente von U, die nicht in A enthalten sind. Notation: Ac oder Ā oder U \ A.

Eingabe der Mengen

Elemente der Teilmenge A

Alle möglichen Elemente (muss A enthalten)
Ergebnis (Ac)
Komplement:
Alle Elemente der Universalmenge, die nicht in A sind

Komplement Info

Eigenschaften

Komplement Ac:

  • Ac = U \ A (Differenz zur Universalmenge)
  • A ∪ Ac = U (Vereinigung ergibt U)
  • A ∩ Ac = ∅ (Schnitt ist leer)
  • (Ac)c = A (Doppeltes Komplement)
Komplement Venn-Diagramm

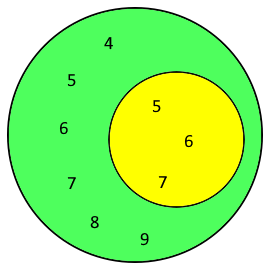
Venn-Diagramm des Komplements

Merksatz: "Das Komplement von A sind alle Elemente der Universalmenge, die nicht in A sind."

Beispiele
Standard:
U = {1,2,3,4,5}, A = {1,3}
Ac = {2,4,5}
Leere Menge:
∅c = U
Universalmenge:
Uc = ∅
Verwandte Operationen

→ Differenzmenge
→ Vereinigungsmenge
→ Schnittmenge

Formeln des Komplements

Grunddefinition
\[A^c = \{x : x \in U \land x \notin A\}\] Mengenschreibweise
Differenzmenge
\[A^c = U \setminus A\] Als Differenzmenge
De Morgan 1
\[(A \cup B)^c = A^c \cap B^c\] Komplement der Vereinigung
De Morgan 2
\[(A \cap B)^c = A^c \cup B^c\] Komplement des Schnitts
Doppeltes Komplement
\[(A^c)^c = A\] Involution
Komplementgesetze
\[A \cup A^c = U\] \[A \cap A^c = \emptyset\] Grundgesetze

Detailliertes Rechenbeispiel

Beispiel: A = {5,6,7}, U = {4,5,6,7,8,9}

Gegeben:

  • A = {5, 6, 7} (Teilmenge)
  • U = {4, 5, 6, 7, 8, 9} (Universalmenge)

Schritt 1 - Prüfung:

A ⊆ U ? {5,6,7} ⊆ {4,5,6,7,8,9} ✓
Alle Elemente von A sind in U enthalten

Schritt 2 - Komplement bestimmen:

4 ∈ U und 4 ∉ A ✓
5 ∈ U und 5 ∈ A ✗
6 ∈ U und 6 ∈ A ✗
7 ∈ U und 7 ∈ A ✗
8 ∈ U und 8 ∉ A ✓
9 ∈ U und 9 ∉ A ✓

Schritt 3 - Ergebnis:

Ac = {4, 8, 9}

Interpretation: Das Komplement von A bezüglich U enthält die Elemente 4, 8, 9, die in der Universalmenge, aber nicht in A sind.

Praktisches Anwendungsbeispiel

Beispiel: Schüler einer Klasse und Wahlfächer

Alle Schüler der Klasse (U):

Anna, Ben, Clara, David, Eva, Franz, Greta, Hans, Ina, Jörg

Französisch-Kurs Teilnehmer (A):

Clara, David, Eva, Hans

Frage: Welche Schüler nehmen NICHT am Französisch-Kurs teil?

Antwort (Ac): Anna, Ben, Franz, Greta, Ina, Jörg

Ergebnis: 6 von 10 Schülern nehmen nicht am Französisch-Kurs teil.

De Morgan'sche Gesetze

Die fundamentalen Gesetze der Mengenlehre
Erstes Gesetz
\[(A \cup B)^c = A^c \cap B^c\]

Das Komplement der Vereinigung ist der Schnitt der Komplemente

Zweites Gesetz
\[(A \cap B)^c = A^c \cup B^c\]

Das Komplement des Schnitts ist die Vereinigung der Komplemente

Praktisches Beispiel

Gegeben: U = {1,2,3,4,5,6}, A = {1,2,3}, B = {3,4,5}

Erstes Gesetz prüfen:
A ∪ B = {1,2,3,4,5}
(A ∪ B)c = {6}

Ac = {4,5,6}, Bc = {1,2,6}
Ac ∩ Bc = {6} ✓
Zweites Gesetz prüfen:
A ∩ B = {3}
(A ∩ B)c = {1,2,4,5,6}

Ac ∪ Bc = {1,2,4,5,6} ✓

Mathematische Eigenschaften

Grundeigenschaften
  • Involution: (Ac)c = A
  • Komplementarität: A ∪ Ac = U
  • Disjunktheit: A ∩ Ac = ∅
  • Eindeutigkeit: Ac ist eindeutig bestimmt
Spezielle Fälle
  • Leere Menge: ∅c = U
  • Universalmenge: Uc = ∅
  • Teilmengen: Wenn A ⊆ B, dann Bc ⊆ Ac
  • Kardinalität: |Ac| = |U| - |A|
Wichtige Hinweise

Universalmenge beachten: Das Komplement ist immer relativ zur gewählten Universalmenge

Teilmengeneigenschaft: A muss eine Teilmenge von U sein

Praktische Anwendungen

Informatik
  • Boolesche Algebra
  • Logische Operationen
  • Datenbank-Abfragen (NOT)
  • Bit-Manipulation
Statistik
  • Komplementärereignisse
  • Wahrscheinlichkeitsrechnung
  • Gegenereignisse
  • Ausschlussverfahren
Verwaltung
  • Ausschlusslisten
  • Nicht-Teilnehmer ermitteln
  • Fehlende Elemente finden
  • Kategorisierung

Mengen Funktionen

Differenzmenge
Komplement
Schnittmenge
Symmetrische Differenz
Vereinigungsmenge