Magnitude Function

Description

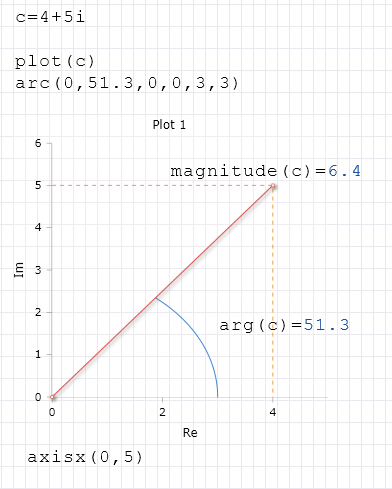
The function \(Magnitude\) returns the magnitude (or absolute value) of a complex number.

The magnitude corresponds to the absolute value of a complex number. It is the distance from the intersection of the x-axis and the y-axis to the two-dimensional point represented by a complex number.

The absolute value is calculated as follows

\( | a + bi | = \sqrt{ (a^2 + b^2)} \)

The magnitude and the phase define the position of a point representing a complex number in the polar coordinate system. You can determine a complex number based on its polar coordinates instead of its Cartesian coordinates by calling the FromPolar function.

Syntax

Magnitude (re + im)

Example

Magnitude(3+4i)= 5

Complex Functions

Arg	Angle of a complex number
Complex	Create complex from two real
Conjugate	Get the conjugate values
FromPolar	Complex number from polar
Im	Gets the imaginary component
Imag	Creates a imaginary number
Magnitude	Gets the magnitude
Plot	Plot of complex numbers
Re	Gets the real component