12dB Frequenzweiche
Berechnung einer Lautsprecher-Frequenzweiche 2. Ordnung mit 12dB Dämpfung pro Oktave
Frequenzweichen-Rechner
12dB Weiche (2. Ordnung)
Frequenzweiche mit zwei Bauteilen pro Weg: Je eine Spule und ein Kondensator für Tieftöner und Hochtöner. Dämpfung: 12dB pro Oktave (Butterworth-Charakteristik).
Schaltplan
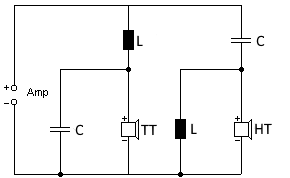
Schaltbild einer 12dB Frequenzweiche (2. Ordnung)
Die berechneten Werte werden automatisch in den Schaltplan eingetragen. Beide Wege verwenden identische Bauteilwerte.
|
|
Berechnungsformeln
Spule (Butterworth 2. Ordnung)
Kondensator (Butterworth 2. Ordnung)
Variablen-Legende
| \(L\) | Spule (Henry) |
| \(C\) | Kondensator (Farad) |
| \(Z\) | Impedanz (Ohm) |
| \(f_C\) | Crossover-Frequenz (Hz) |
| \(\sqrt{2}\) | Butterworth-Faktor ≈ 1,414 |
Phasenverhalten
Bei 12dB Weichen bewegen sich beide Lautsprecher in Phase. Keine Umpolung erforderlich!
Eigenschaften der 12dB Weiche (2. Ordnung)
Funktionsweise
Eine Frequenzweiche 2. Ordnung benötigt 2 Bauteile in jedem Zweig und bietet eine Flankensteilheit von 12dB pro Oktave. Die Werte der Kondensatoren und Spulen im Hoch- und Tiefpass sind identisch. Diese Weiche basiert auf der Butterworth-Charakteristik mit einem Q-Faktor von 0,707.
Vorteile
- Bessere Trennung (12dB/Oktave)
- Standard für HiFi-Anwendungen
- Keine Umpolung erforderlich
- Flacher Frequenzgang
Nachteile
- Mehr Bauteile erforderlich
- Höhere Kosten
- Komplexere Schaltung
- Höhere Verluste
Technische Details
Phasenverhalten
Da im Tiefpass bei der Übernahmefrequenz der Strom gegenüber der Spannung um 180° nacheilt und am Hochpass die Spannung gegenüber dem Strom ebenfalls um 180° nacheilt, bewegen sich die Membranen der Lautsprecher in Phase.
Butterworth-Charakteristik
Die 12dB Weiche verwendet die Butterworth-Charakteristik mit einem Q-Faktor von 0,707. Dies ergibt einen maximally flat response im Durchlassbereich.
Typische Anwendung
12dB Weichen sind der Standard für hochwertige HiFi-Lautsprecher. Sie bieten eine gute Balance zwischen Trennschärfe und Phasenverhalten.
Berechnungsbeispiel
Gegeben: 8Ω Lautsprecher, Trennfrequenz 2400Hz
\[L = \frac{\sqrt{2} \cdot 8Ω}{2π \times 2400Hz} ≈ 0,75\text{ mH}\]
\[C = \frac{\sqrt{2}}{4π \times 2400Hz \times 8Ω} ≈ 5,9\text{ µF}\]
Vergleich der Weichen-Ordnungen
| Ordnung | Dämpfung | Bauteile pro Weg | Phasenverhalten | Anwendung |
|---|---|---|---|---|
| 1. Ordnung | 6dB/Oktave | 1 (L oder C) | Umpolung nötig | Einfache Systeme |
| 2. Ordnung | 12dB/Oktave | 2 (L und C) | Keine Umpolung | HiFi-Standard |
| 3. Ordnung | 18dB/Oktave | 3 (L-C-L oder C-L-C) | Umpolung nötig | Professionell |