Calculate RLC Series Circuit

Calculator and formulas for calculating voltage and power of an RLC series circuit

Calculate RLC Series Circuit

RLC Series Circuit

The calculator computes voltages, powers, current, impedance and reactance in the series circuit of a resistor, an inductor and a capacitor.

Results
Reactance XL:
Reactance XC:
Total impedance Z:
Inductor voltage UL:
Capacitor voltage UC:
Resistor voltage UR:
Current I:
Active power P:
Reactive power QL:
Reactive power QC:
Apparent power S:
Phase angle φ:

RLC Series Circuit

LCR Series Circuit, RLC Series Circuit
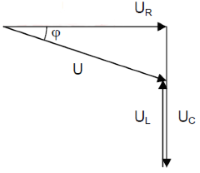
Series Circuit Properties
  • Same current through all components
  • Geometric addition of component voltages
  • UL and UC are 180° out of phase
  • Phase shift between 0° and ±90°
Basic Formulas
\[U=\sqrt{U_R^2+(U_L-U_C)^2}\] \[Z=\sqrt{R^2+(X_L-X_C)^2}\]

Voltage and impedance triangle according to Pythagoras

Phase Relationships
  • R: Current and voltage in phase
  • L: Voltage leads by +90°
  • C: Voltage lags by -90°
  • Resulting phase: Depends on XL - XC

RLC Series Circuit - Theory and Formulas

Fundamentals of RLC Series Circuit

The total resistance of the RLC series circuit in the AC circuit is called impedance Z. Ohm's law applies to the complete circuit. The current is the same at every measurement point.

Voltage Triangle

Voltages
\[U=\sqrt{U_R^2+(U_L-U_C)^2}\] \[\phi=\arctan\left(\frac{U_L-U_C}{U_R}\right)\]
UL = Voltage across the inductor
UC = Voltage across the capacitor
UR = Voltage across the resistor
U = Applied voltage
Impedance Triangle
\[Z=\sqrt{R^2+(X_L-X_C)^2}\] \[\phi=\arccos\left(\frac{R}{Z}\right)\]
Z = Impedance
R = Ohmic resistance
XL = Inductive reactance
XC = Capacitive reactance

Reactances and Current

Reactances
\[X_L = 2\pi f L\] \[X_C = \frac{1}{2\pi f C}\]

Frequency-dependent resistances of inductor and capacitor.

Current
\[I = \frac{U}{Z}\]

Current is the same in all components (series circuit).

Component Voltages
\[U_R = I \cdot R\] \[U_L = I \cdot X_L\] \[U_C = I \cdot X_C\]

Voltages across individual components.

Power Triangle

Powers
\[S=\sqrt{P^2+(Q_L-Q_C)^2}\] \[\phi=\arccos\left(\frac{P}{S}\right)\]
\[P = I \cdot U_R\] \[Q_L = I \cdot U_L\] \[Q_C = I \cdot U_C\]
P = Active power, S = Apparent power
QL = Inductive reactive power, QC = Capacitive reactive power

Frequency Behavior

Low Frequencies
  • XC >> XL
  • Capacitive behavior
  • Negative phase shift
  • High impedance
Resonance Frequency
  • XL = XC
  • Z = R (minimum)
  • φ = 0°
  • Maximum current
High Frequencies
  • XL >> XC
  • Inductive behavior
  • Positive phase shift
  • High impedance

Practical Applications

Filter circuits:
• Bandpass filters
• Notch filters
• Crossover networks
• Matching networks
Resonant circuits:
• Resonance circuits
• Oscillator tanks
• Tuned circuits
• Filter design
Power electronics:
• Resonant converters
• Induction heating
• Wireless power
• Resonant power supplies

Design Guidelines

Important Design Aspects
  • Resonance: At f₀ = 1/(2π√LC), Z is minimum
  • Voltage enhancement: UL and UC can exceed U
  • Quality factor: Q = (XL or XC)/R at resonance
  • Losses: Consider ESR of components
  • Temperature effects: L and C are temperature dependent
  • Tolerances: Significantly affect resonance frequency


Other LC calculators

Resonant frequency f0 calculator  •  Resistors-capacitors-inductors series circuit  •  Resistors-capacitors-inductors parallel circuit  •  Resonance of RCL parallel circuit  •  Resonance of RCL series circuit  •