RLC Reihenschaltung berechnen
Rechner und Formeln zur Berechnung von Spannung und Leistung einer RLC Reihenschaltung
RLC Reihenschaltung berechnen
RLC Serienschaltung
Der Rechner berechnet die Spannungen, Leistungen, Strom, Schein- und Blindwiderstand in der Reihenschaltung eines Widerstands, einer Spule und eines Kondensators.
RLC Serienschaltung
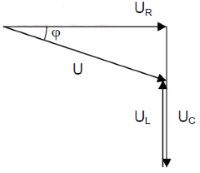
Serienschaltung Eigenschaften
- Gleicher Strom durch alle Bauteile
- Geometrische Addition der Teilspannungen
- UL und UC sind um 180° phasenverschoben
- Phasenverschiebung zwischen 0° und ±90°
Grundformeln
Spannungs- und Widerstandsdreieck nach Pythagoras
Phasenbeziehungen
- R: Strom und Spannung in Phase
- L: Spannung eilt um +90° voraus
- C: Spannung eilt um -90° nach
- Resultierende Phase: Abhängig von XL - XC
|
|
|
|
RLC Serienschaltung - Theorie und Formeln
Grundlagen der RLC Serienschaltung
Der Gesamtwiderstand der RLC-Reihenschaltung im Wechselstromkreis wird als Scheinwiderstand oder Impedanz Z bezeichnet. Für die Gesamtschaltung gilt das Ohmsche Gesetz. Der Strom ist an jeder Messstelle gleich.
Spannungsdreieck
Spannungen
Widerstandsdreieck
Blindwiderstände und Strom
Blindwiderstände
Frequenzabhängige Widerstände von Spule und Kondensator.
Strom
Strom ist in allen Komponenten gleich (Serienschaltung).
Teilspannungen
Spannungen an den einzelnen Komponenten.
Leistungsdreieck
Leistungen
Frequenzverhalten
Tiefe Frequenzen
- XC >> XL
- Kapazitives Verhalten
- Negative Phasenverschiebung
- Hohe Impedanz
Resonanzfrequenz
- XL = XC
- Z = R (minimal)
- φ = 0°
- Maximaler Strom
Hohe Frequenzen
- XL >> XC
- Induktives Verhalten
- Positive Phasenverschiebung
- Hohe Impedanz
Praktische Anwendungen
Filter-Schaltungen:
Schwingkreise:
Leistungselektronik:
Design-Hinweise
Wichtige Designaspekte
- Resonanz: Bei f₀ = 1/(2π√LC) ist Z minimal
- Spannungsüberhöhung: UL und UC können U überschreiten
- Güte: Q = (XL oder XC)/R bei Resonanz
- Verluste: ESR der Bauteile beachten
- Temperatureinfluss: L und C sind temperaturabhängig
- Toleranzen: Beeinflussen Resonanzfrequenz erheblich
|
|