Calculate Trapezoid Diagonal e
Calculator and formulas for trapezoid diagonal e using side lengths and height
Trapezoid Diagonal e Calculator
Trapezoid Diagonal
A trapezoid has two parallel sides. The diagonal e connects two non-adjacent vertices and can be calculated from the side lengths and height.
Trapezoid with Diagonal e
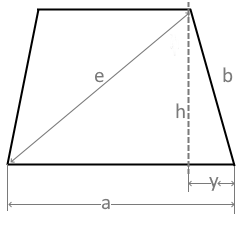
The diagram shows a trapezoid with sides a and b, height h and diagonal e.
Diagonal e connects two non-adjacent vertices.
|
|
What is a Trapezoid?
A trapezoid is a quadrilateral with special properties:
- Two parallel sides: The bases are parallel to each other
- Different lengths: The parallel sides usually have different lengths
- Oblique sides: The non-parallel sides connect the bases
- Height: The perpendicular distance between the parallel sides
- Diagonals: Connecting lines between non-adjacent vertices
- Applications: Architecture, engineering, roof construction
Diagonal e in a Trapezoid
The diagonal e is an important quantity in trapezoid geometry:
Definition
- Connects two non-adjacent vertices
- Divides the trapezoid into two triangles
- One of two possible diagonals
- Length depends on side lengths and height
Calculation
- Pythagorean theorem in right-angled sub-triangle
- Coordinate geometry possible
- Trigonometric relationships
- Vector calculation as alternative
Practical Applications
Trapezoid diagonals are important in many practical areas:
Construction & Architecture
- Roof constructions and gables
- Bridge construction and load-bearing structures
- Bracing and stiffening
- Trapezoidal windows and doors
Engineering & Design
- Mechanical engineering: wedge connections
- Vehicle construction: body parts
- Furniture design: geometric shapes
- Landscape design: beds and pathways
Calculation Methods
Diagonal e can be calculated in various ways:
Pythagorean
Use right-angled sub-triangle
Coordinates
Cartesian coordinate system
Trigonometry
Angles and trigonometric functions
Formulas for Calculating Diagonal e
Main Formula with sides a, b and height h
Where: \(y = \sqrt{b^2 - h^2}\)
Calculation of y
Horizontal distance of the oblique side
Alternative with sides c, d
With \(x = \sqrt{d^2 - h^2}\)
Coordinate Method
Euclidean distance between vertices
With angle β
Law of cosines in trapezoid sub-triangle
Step-by-Step Calculation
\(y = \sqrt{b^2 - h^2}\)
Horizontal projection of side b
\(e = \sqrt{(a-y)^2 + h^2}\)
Pythagorean theorem in right triangle
Notation in Trapezoid
- a: Parallel side (often the upper/shorter one)
- b: Oblique side of the trapezoid
- c: Lower parallel side (often longer)
- d: Other oblique side
- h: Height (distance between parallel sides)
- e: First diagonal
- f: Second diagonal
- y, x: Horizontal projections of oblique sides
Calculation Example
Given
Find: Diagonal e
1. Calculate y
Horizontal projection of oblique side b
2. Calculate diagonal e
Pythagorean theorem in right sub-triangle
3. Result
Diagonal e has a length of approximately 5.66 units
4. Verification
Verification using coordinate geometry:
Vertices: A(0,0), B(7,0), C(3,4), D(0,4)
Diagonal AC: \(\sqrt{(7-0)^2 + (0-4)^2} = \sqrt{49+16} = \sqrt{65} \approx 8.06\)
Diagonal BD: \(\sqrt{(3-0)^2 + (4-0)^2} = \sqrt{9+16} = \sqrt{25} = 5\)
Note: Depending on the orientation of the trapezoid, different diagonal lengths result.
The Trapezoid and Its Diagonals in Mathematics and Practice
The trapezoid is a fascinating geometric object characterized by its two parallel sides. The diagonals of a trapezoid play an important role in geometry and have practical significance in architecture, engineering, and design.
Definition and Basic Properties of Trapezoids
A trapezoid is a quadrilateral with special properties:
- Two parallel sides: The bases are parallel to each other
- Two non-parallel sides: The legs connect the parallel sides
- Height: The perpendicular distance between the parallel sides
- Two diagonals: Connecting lines between non-adjacent vertices
- Various forms: Isosceles, right-angled or general
The Diagonals - Geometric Significance
The diagonals of a trapezoid have special geometric properties:
Structural Properties
Diagonals divide the trapezoid into four triangles, where opposite triangles are similar.
Intersection Behavior
The diagonals intersect inside the trapezoid and divide in characteristic ratios.
Length Relationships
The lengths of the diagonals are directly related to the side lengths and height of the trapezoid.
Symmetry Properties
In isosceles trapezoids both diagonals are equal in length, in general trapezoids usually different.
Practical Applications
Trapezoid diagonals find application in many practical areas:
Construction and Engineering
- Roof constructions: rafters and bracing
- Bridge building: truss constructions
- Steel construction: stiffening diagonals
- Wood construction: frame connections
Mechanical Engineering
- Gear technology: wedge connections
- Vehicle construction: chassis reinforcements
- Conveyor technology: bulk material containers
- Machine tools: guide rails
Design and Architecture
- Windows and doors: trapezoidal openings
- Furniture design: modern geometric forms
- Landscape architecture: beds and pathways
- Interior design: room division
Technology and Electronics
- Optics: prism geometry
- Electronics: circuit board shapes
- Solar technology: panel alignment
- Antenna technology: directional beam geometry
Calculation Methods in Detail
The calculation of trapezoid diagonals can be done in various ways:
Pythagorean Method
The classical method uses right-angled sub-triangles. By projecting the oblique sides, right triangles are created where the Pythagorean theorem can be applied.
Coordinate Geometry
Placing the trapezoid in a coordinate system enables calculation via the distance formula between vertices.
Trigonometric Methods
With known angles, the diagonal can be calculated using sine, cosine, or tangent functions.
Vector Calculation
Modern method with vectors enables elegant calculations and is particularly advantageous in 3D applications.
Mathematical Relationships
Trapezoid diagonals follow interesting mathematical patterns:
- Diagonal theorem: In a trapezoid with parallel sides a and c, the diagonals intersect to form similar triangles
- Length ratios: The ratios of diagonal segments correspond to the ratios of the parallel sides
- Area relationships: The diagonals divide the trapezoid into four triangles with special area ratios
- Midline: The midline connects the midpoints of the non-parallel sides and is parallel to the bases
- Symmetry properties: Additional symmetry relationships apply to isosceles trapezoids
Special Types of Trapezoids
Isosceles Trapezoid
Both non-parallel sides are equal in length. The diagonals have equal length and the trapezoid is axially symmetric.
Right Trapezoid
One of the non-parallel sides is perpendicular to the parallel sides. Significantly simplifies calculation.
Scalene Trapezoid
General form without special symmetries. The diagonals usually have different lengths.
Parallelogram
Special case with two pairs of parallel sides. Both diagonals intersect at their midpoints.
Historical and Cultural Significance
The trapezoid has a rich history in various cultures:
- Ancient geometry: Already used by Babylonians for area calculations
- Egyptian mathematics: Truncated pyramids as three-dimensional trapezoid applications
- Greek geometry: Systematic investigation by Euclid and others
- Roman engineering: Application in aqueducts and architecture
- Medieval architecture: Gothic arches and window forms
- Renaissance: Perspective and spatial representation
- Modern era: Engineering applications and computer graphics
Related Geometric Concepts
The trapezoid is related to other geometric shapes:
- Triangles: Trapezoids can be viewed as composite triangles
- Parallelograms: Special cases of trapezoids with two pairs of parallel sides
- Quadrilaterals in general: Trapezoids as a special class of quadrilaterals
- Circle sectors: Relationship in area calculation
- Polygons: Trapezoids as building blocks of more complex polygons
Summary
The diagonal e of a trapezoid is more than just a geometric quantity. It connects mathematical theory with practical applications and shows how simple geometric concepts are used in complex technical and architectural solutions. The various calculation methods demonstrate the versatility of mathematics and its applicability in different contexts.
|
|
|
|