Calculate Trapezoid Diagonal f with Angle
Calculator and formulas for trapezoid diagonal f using side lengths and angle α
Trapezoid Diagonal f (Angle α Method)
Angle-based calculation of the second diagonal
The diagonal f can, with known side lengths a and d and the angle α, be calculated directly using the law of cosines without needing the height.
Trapezoid with Angle α
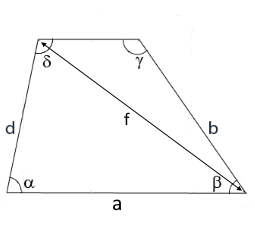
The diagram shows a trapezoid with sides a and d and angle α.
Diagonal f is calculated using the law of cosines.
|
|
Angle-based calculation of diagonal f
The second diagonal f can be computed analogously to diagonal e using angles:
- Different side combination: Uses sides a and d instead of a and b
- Angle α: Included angle between a and d
- Law of cosines: Direct approach without height calculation
- Flexibility: Works for various trapezoid shapes
- Alternative: Substitute for height-based calculation
- Application: Particularly useful in surveying
The angle α for diagonal f
The angle α between sides a and d determines the length of diagonal f:
Definition
- Angle between sides a and d
- Usually different from angle β for diagonal e
- Measured in degrees (°) or radians
- Determines trapezoid geometry
Influence on diagonal f
- Cosine of the angle determines the length
- At α=90° it corresponds to the Pythagorean theorem
- Acute angles give longer diagonals
- Obtuse angles shorten the diagonal
Law of cosines for diagonal f
The law of cosines enables direct calculation of diagonal f:
Formula
Analogous to the formula for diagonal e
Application
- Same mathematical basis as for e
- Different side combination (a, d instead of a, b)
- Different angle (α instead of β)
- Usually different diagonal length
Formulas for angle-based calculation of diagonal f
Main formula: Law of cosines for diagonal f
Diagonal f from sides a, d and the included angle α
Angle in radians
Conversion from degrees to radians
Special case α = 90°
Reduces to the Pythagorean theorem
Alternative with sides c, b
With other sides and angle γ
Comparison with diagonal e
Analogous with sides a, b and angle β
Height-based alternative
\(x = \sqrt{d^2 - h^2}\)
Horizontal projection of side d
\(f = \sqrt{(a-x)^2 + h^2}\)
Pythagorean theorem in a right triangle
Calculation Example
Given
Find: Diagonal f
1. Calculate cosine
Known trigonometric value
2. Substitute values
Apply the law of cosines
3. Final result
Diagonal f has a length of approximately 5.57 units
4. Comparison with diagonal e
Calculation of diagonal e (assume b = 5, β = 60°):
\(e^2 = 6^2 + 5^2 - 2 \cdot 6 \cdot 5 \cdot \cos(60°) = 36 + 25 - 30 = 31\)
\(e = \sqrt{31} \approx 5.57\)
In this example both diagonals are equal because d = b and α = β.
Plausibility check: For α=60° cos(60°) = 0.5 > 0, therefore f < √(a²+d²) = √61 ≈ 7.81 ✓
Angle-based calculation of diagonal f in theory and practice
The angle-based calculation of diagonal f completes the geometric understanding of trapezoid diagonals. As the second diagonal it complements diagonal e and together they provide a complete characterization of the trapezoid's internal structure. The law of cosines provides an elegant direct computation here as well.
Diagonal f - properties and significance
Diagonal f is the second main diagonal of the trapezoid and differs from e:
- Alternative connection: Connects the other two non-adjacent vertices
- Different side basis: Uses sides a and d instead of a and b
- Different angle: Angle α between a and d is usually different from β
- Different length: In general trapezoids f ≠ e
- Equality only with symmetry: f = e only in isosceles trapezoids
The angle α in context
The angle α plays a central role in characterizing the trapezoid:
Geometric meaning
The angle α between sides a and d, together with the side lengths, determines the trapezoid's shape and the length of diagonal f.
Relation to other angles
In a trapezoid the angles are linked by the parallel bases. The sum of all interior angles is 360°.
Practical measurability
Angles are often easier to measure than heights, especially for large structures or in surveying.
Constructive specification
In practice angles are often provided as design parameters from which other quantities are derived.
Practical applications
Angle-based calculation of diagonal f finds application in many areas:
Structural engineering
- Trusses: Both diagonals for maximum stability
- Bridge construction: Cross bracing
- Steel structures: Redundant load paths
- High-rise buildings: Frame stiffening
Surveying and cartography
- Triangulation: Both diagonals for accuracy
- Area surveying: Complete trapezoid characterization
- GPS measurements: Redundant determination
- Cadastral surveying: Precise boundary determination
Design and architecture
- Modern architecture: Asymmetric design
- Roof structures: Different rafter directions
- Interior design: Dynamic space division
- Landscape architecture: Complex pathway planning
Mechanical engineering and technology
- Gear technology: Multi-directional force transmission
- Robotics: Complex joint kinematics
- Vehicle construction: Chassis stiffening
- Optics: Prism geometry
Summary
Angle-based calculation of diagonal f completes the geometric understanding of trapezoids. Together with diagonal e it enables a full characterization of trapezoid geometry. The law of cosines offers an elegant and direct computational path, which is particularly valuable in modern engineering and computer-aided design.
|
|
|
|