Resistors in Series

Understand series circuits and how to calculate total resistance, current, and voltage distribution

Overview

In a series connection, multiple resistors are connected in a line, so the current flows through each resistor in sequence. The same current flows through all resistors in a series circuit.

Characteristic:

The same current flows through all resistors, but the voltage divides across them proportionally to their resistance values. This is opposite to parallel circuits.

Total Resistance

In a series circuit, the total resistance is simply the sum of all individual resistances.

Key Principle:

Resistances add directly in series. Adding more resistors always increases the total resistance.

\(\displaystyle R_{\text{total}} = R_1 + R_2 + R_3 + \ldots\)

Key observation

The total resistance in a series circuit is always greater than any individual resistance. Each resistor adds to the total resistance.

Current in Series Circuit

The same current flows through all resistors in a series circuit. Using Ohm's Law, we can calculate this current from the total voltage and total resistance.

Current Rule:

The total current through all resistors is identical:

\(\displaystyle I_{\text{total}} = I_1 = I_2 = I_3 = \ldots\)

Using Ohm's Law with total values:

\(\displaystyle I = \frac{U_{\text{total}}}{R_{\text{total}}}\)

Voltage Division in Series

In a series circuit, the total voltage divides across the individual resistors. The voltage distribution is proportional to the resistance values.

Voltage Sum Rule

The total voltage is the sum of the individual voltages:

\(\displaystyle U_{\text{total}} = U_1 + U_2 + U_3 + \ldots\)

Voltage Divider Principle

The voltage across each resistor is proportional to its resistance. The ratio of voltages equals the ratio of resistances:

\(\displaystyle \frac{U_{\text{total}}}{R_{\text{total}}} = \frac{U_1}{R_1} = \frac{U_2}{R_2} = \frac{U_3}{R_3}\)

Individual Voltage Formulas

The voltage across a specific resistor can be calculated in two ways:

Method 1: Using Current

\(\displaystyle U_1 = R_1 \cdot I\)

Method 2: Using Ratio

\(\displaystyle U_1 = \frac{R_1 \cdot U_{\text{total}}}{R_{\text{total}}}\)

Worked Example

Calculate Series Resistor Circuit

Given:

\(R_1 = 20\,\Omega\)
\(R_2 = 40\,\Omega\)
\(R_3 = 55\,\Omega\)
\(U_{\text{total}} = 230\,\text{V}\)

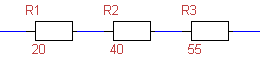
Step 1: Calculate total resistance

\(\displaystyle R_{\text{total}} = R_1 + R_2 + R_3 = 20 + 40 + 55 = 115\,\Omega\)

Step 2: Calculate total current

\(\displaystyle I = \frac{U_{\text{total}}}{R_{\text{total}}} = \frac{230}{115} = 2\,\text{A}\)

Step 3: Calculate individual voltages

Voltage across \(R_1\):

Method 1: \(\displaystyle U_1 = R_1 \cdot I = 20 \cdot 2 = 40\,\text{V}\)

Method 2: \(\displaystyle U_1 = \frac{R_1 \cdot U_{\text{total}}}{R_{\text{total}}} = \frac{20 \cdot 230}{115} = 40\,\text{V}\)

Voltage across \(R_2\):

Method 1: \(\displaystyle U_2 = R_2 \cdot I = 40 \cdot 2 = 80\,\text{V}\)

Method 2: \(\displaystyle U_2 = \frac{R_2 \cdot U_{\text{total}}}{R_{\text{total}}} = \frac{40 \cdot 230}{115} = 80\,\text{V}\)

Voltage across \(R_3\):

Method 1: \(\displaystyle U_3 = R_3 \cdot I = 55 \cdot 2 = 110\,\text{V}\)

Method 2: \(\displaystyle U_3 = \frac{R_3 \cdot U_{\text{total}}}{R_{\text{total}}} = \frac{55 \cdot 230}{115} = 110\,\text{V}\)

Verification:

\(\displaystyle U_1 + U_2 + U_3 = 40 + 80 + 110 = 230\,\text{V}\) ✓

Summary: Series vs Parallel

Series Circuit

Resistance: \(R = R_1 + R_2 + \ldots\)
Current: Same everywhere
Voltage: Divides proportionally

Parallel Circuit

Resistance: \(\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \ldots\)
Current: Divides proportionally
Voltage: Same everywhere

Key Properties of Series Circuits

Same current flows through all resistors
Total resistance is sum of individual resistances
Total voltage is sum of individual voltages
Voltage divides proportionally to resistance values
Higher resistance resistor gets higher voltage drop
Total resistance is always greater than any individual resistor
If one component fails (opens), the entire circuit breaks

Resistors in Parallel
Resistors in Series
Resistor Color Coding

Is this page helpful?

Thank you for your feedback!

Sorry about that
How can we improve it?