Differenzmenge

Rechner zur Berechnung der Differenzmenge mit ausführlichen Formeln und Beispielen

Differenzmenge Rechner

Was wird berechnet?

Die Differenzmenge A \ B enthält alle Elemente, die in der ersten Menge A enthalten sind, aber nicht in der zweiten Menge B vorkommen.

Eingabe der Mengen

Werte durch Leerzeichen oder Semikolon getrennt

Werte durch Leerzeichen oder Semikolon getrennt
Ergebnis (A \ B)
Differenzmenge:
Enthält nur Elemente aus Menge A, die nicht in B sind

Differenzmenge Info

Eigenschaften

Differenzmenge A \ B:

  • Enthält nur Elemente aus A
  • Schließt alle Elemente aus B aus
  • Ist nicht kommutativ: A \ B ≠ B \ A
  • Kann leer sein: ∅
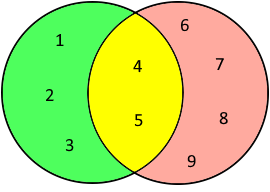
Differenzmenge Venn-Diagramm

Venn-Diagramm der Differenzmenge

Merksatz: "A minus B sind alle A-Elemente ohne die B-Elemente."

Beispiele
Standard:
{1,2,3} \ {2,3,4} = {1}
Disjunkt:
{1,2} \ {3,4} = {1,2}
Teilmenge:
{1,2,3} \ {1,2} = {3}
Verwandte Operationen

→ Vereinigungsmenge
→ Schnittmenge
→ Symmetrische Differenz


Formeln der Differenzmenge

Grunddefinition
\[A \setminus B = \{x : x \in A \land x \notin B\}\] Standard-Differenzmenge
Alternative Schreibweise
\[A \setminus B = A \cap \overline{B}\] Schnitt mit dem Komplement
Symmetrische Differenz
\[A \triangle B = (A \setminus B) \cup (B \setminus A)\] Beidseitige Differenz
Relative Komplement
\[A \setminus B = A \cap B^c\] Schnitt mit Komplement
Kommutativität
\[A \setminus B \neq B \setminus A\] Nicht kommutativ
Assoziativität
\[(A \setminus B) \setminus C \neq A \setminus (B \setminus C)\] Nicht assoziativ

Detailliertes Rechenbeispiel

Beispiel: A = {1,2,3,4,5}, B = {4,5,6,7,8,9}

Gegeben:

  • A = {1, 2, 3, 4, 5}
  • B = {4, 5, 6, 7, 8, 9}

Schritt 1 - Elemente aus A prüfen:

1 ∈ A und 1 ∉ B ✓
2 ∈ A und 2 ∉ B ✓
3 ∈ A und 3 ∉ B ✓
4 ∈ A und 4 ∈ B ✗
5 ∈ A und 5 ∈ B ✗

Schritt 2 - Ergebnis:

A \ B = {1, 2, 3}

Vergleich B \ A:

B \ A = {6, 7, 8, 9}

Interpretation: Die Differenzmenge A \ B enthält nur die Elemente 1, 2, 3, die ausschließlich in A vorkommen.

Praktisches Anwendungsbeispiel

Beispiel: Mitgliederverwaltung in einem Verein

Alle Mitglieder (A):

Anna, Ben, Clara, David, Eva, Franz, Greta, Hans

Zahlende Mitglieder (B):

Clara, David, Eva, Franz, Ines, Jörg

Frage: Welche Mitglieder haben noch nicht bezahlt?

Antwort (A \ B): Anna, Ben, Greta, Hans

Ergebnis: 4 Mitglieder müssen noch ihre Beiträge zahlen.

Gesetze der Differenzmenge

Wichtige Eigenschaften und Gesetze
Identität
\[A \setminus \emptyset = A\]

Differenz mit leerer Menge

Selbstdifferenz
\[A \setminus A = \emptyset\]

Menge minus sich selbst

Distributivität
\[A \setminus (B \cup C) = (A \setminus B) \cap (A \setminus C)\]

Verteilung über Vereinigung

De Morgan
\[A \setminus (B \cap C) = (A \setminus B) \cup (A \setminus C)\]

Verteilung über Schnitt

Wichtig: Die Differenzmenge ist weder kommutativ noch assoziativ!

Mathematische Eigenschaften

Grundeigenschaften
  • Eindeutigkeit: A \ B ist eindeutig bestimmt
  • Teilmenge: A \ B ⊆ A (immer)
  • Disjunktheit: (A \ B) ∩ B = ∅
  • Kardinalität: |A \ B| ≤ |A|
Besondere Eigenschaften
  • Nicht kommutativ: A \ B ≠ B \ A
  • Nicht assoziativ: (A \ B) \ C ≠ A \ (B \ C)
  • Monotonie: Wenn B ⊆ C, dann A \ C ⊆ A \ B
  • Komplement-Bezug: A \ B = A ∩ B̄
Praktische Hinweise

Reihenfolge beachten: A \ B ist nicht das gleiche wie B \ A

Visualisierung: Venn-Diagramme helfen beim Verständnis

Praktische Anwendungen

Datenbanken
  • SQL EXCEPT Operationen
  • Datenbereinigung
  • Duplikatentfernung
  • Differenzanalysen
Verwaltung
  • Mitgliederverwaltung
  • Teilnehmerlisten
  • Bestandsvergleiche
  • Fehlende Elemente finden
Programmierung
  • Set-Operationen
  • Filter-Algorithmen
  • Ausschlusslogik
  • Differenz-Berechnungen




Mengen Funktionen

Differenzmenge
Komplement
Schnittmenge
Symmetrische Differenz
Vereinigungsmenge