Schnittmenge

Rechner zur Berechnung der Schnittmenge mit ausführlichen Formeln und Beispielen

Schnittmenge Rechner

Was wird berechnet?

Die Schnittmenge A ∩ B enthält alle Elemente, die sowohl in Menge A als auch in Menge B enthalten sind. Sie ist das "Gemeinsame" beider Mengen.

Eingabe der Mengen

Werte durch Leerzeichen oder Semikolon getrennt

Werte durch Leerzeichen oder Semikolon getrennt
Ergebnis (A ∩ B)
Schnittmenge:
Elemente, die in beiden Mengen vorkommen

Schnittmenge Info

Eigenschaften

Schnittmenge A ∩ B:

  • Kommutativ: A ∩ B = B ∩ A
  • Assoziativ: (A ∩ B) ∩ C = A ∩ (B ∩ C)
  • Idempotent: A ∩ A = A
  • A ∩ B ⊆ A und A ∩ B ⊆ B
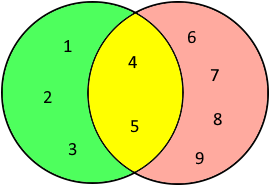
Schnittmenge Venn-Diagramm

Venn-Diagramm der Schnittmenge

Merksatz: "Die Schnittmenge enthält nur die Elemente, die in beiden Mengen gleichzeitig vorkommen."

Beispiele
Standard:
{1,2,3} ∩ {2,3,4} = {2,3}
Disjunkt:
{1,2} ∩ {3,4} = ∅
Teilmenge:
{1,2} ∩ {1,2,3} = {1,2}
Verwandte Operationen

→ Vereinigungsmenge
→ Differenzmenge
→ Symmetrische Differenz


Formeln der Schnittmenge

Grunddefinition
\[A \cap B = \{x : x \in A \land x \in B\}\] Mengenschreibweise
Kommutativgesetz
\[A \cap B = B \cap A\] Reihenfolge beliebig
Assoziativgesetz
\[(A \cap B) \cap C = A \cap (B \cap C)\] Klammerung beliebig
Distributivgesetze
\[A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\] Verteilung über Vereinigung
Idempotenz
\[A \cap A = A\] Selbstschnitt
Neutrale Elemente
\[A \cap U = A\] \[A \cap \emptyset = \emptyset\] Mit Universalmenge und leerer Menge

Detailliertes Rechenbeispiel

Beispiel: A = {1,2,3,4,5}, B = {4,5,6,7,8,9}

Gegeben:

  • A = {1, 2, 3, 4, 5}
  • B = {4, 5, 6, 7, 8, 9}

Schritt 1 - Elemente prüfen:

1 ∈ A, aber 1 ∉ B ✗
2 ∈ A, aber 2 ∉ B ✗
3 ∈ A, aber 3 ∉ B ✗
4 ∈ A und 4 ∈ B ✓
5 ∈ A und 5 ∈ B ✓

Schritt 2 - Gemeinsame Elemente:

A ∩ B = {4, 5}

Verifikation:

B ∩ A = {4, 5} ✓ (kommutativ)
|A ∩ B| = 2 Elemente

Interpretation: Die Schnittmenge enthält nur die Elemente 4 und 5, da diese die einzigen sind, die in beiden Mengen vorkommen.

Praktisches Anwendungsbeispiel

Beispiel: Gemeinsame Hobbys von Freunden

Annas Hobbys (A):

Lesen, Schwimmen, Radfahren, Kochen, Malen

Bens Hobbys (B):

Schwimmen, Wandern, Kochen, Gaming, Fotografie

Frage: Welche Hobbys haben Anna und Ben gemeinsam?

Antwort (A ∩ B): {Schwimmen, Kochen}

Ergebnis: Anna und Ben haben 2 gemeinsame Hobbys, bei denen sie zusammen Aktivitäten unternehmen können.

Gesetze der Schnittmenge

Fundamentale Gesetze der Mengenlehre
Kommutativgesetz
\[A \cap B = B \cap A\]

Reihenfolge spielt keine Rolle

Assoziativgesetz
\[(A \cap B) \cap C = A \cap (B \cap C)\]

Klammerung beliebig

Distributivgesetz
\[A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\]

Verteilung über Vereinigung

Absorptionsgesetz
\[A \cap (A \cup B) = A\]

Absorption der Vereinigung

Beispiel für Distributivgesetz

Gegeben: A = {1,2}, B = {2,3}, C = {3,4}

Linke Seite:
B ∪ C = {2,3,4}
A ∩ (B ∪ C) = {1,2} ∩ {2,3,4} = {2}
Rechte Seite:
A ∩ B = {2}, A ∩ C = ∅
(A ∩ B) ∪ (A ∩ C) = {2} ∪ ∅ = {2} ✓

Mathematische Eigenschaften

Grundeigenschaften
  • Teilmenge: A ∩ B ⊆ A und A ∩ B ⊆ B
  • Kommutativität: A ∩ B = B ∩ A
  • Assoziativität: (A ∩ B) ∩ C = A ∩ (B ∩ C)
  • Idempotenz: A ∩ A = A
Spezielle Eigenschaften
  • Leere Menge: A ∩ ∅ = ∅
  • Universalmenge: A ∩ U = A
  • Komplement: A ∩ Ac = ∅
  • Kardinalität: |A ∩ B| ≤ min(|A|, |B|)
Wichtige Hinweise

Disjunkte Mengen: Wenn A ∩ B = ∅, dann sind A und B disjunkt

Größte untere Schranke: A ∩ B ist die größte Menge, die in beiden enthalten ist

Praktische Anwendungen

Datenbanken
  • SQL INTERSECT Operationen
  • JOIN-Verknüpfungen
  • Gemeinsame Datensätze finden
  • Überschneidungsanalysen
Soziale Analysen
  • Gemeinsame Freunde
  • Überschneidende Interessen
  • Geteilte Eigenschaften
  • Gruppenschnittmengen
Datenanalyse
  • Überlappende Kategorien
  • Gemeinsame Merkmale
  • Filteroperationen
  • Korrelationsanalysen




Mengen Funktionen

Differenzmenge
Komplement
Schnittmenge
Symmetrische Differenz
Vereinigungsmenge