Vereinigungsmenge

Rechner zur Berechnung der Vereinigungsmenge mit ausführlichen Formeln und Beispielen

Vereinigungsmenge Rechner

Was wird berechnet?

Die Vereinigungsmenge A ∪ B enthält alle Elemente, die mindestens in einer der beiden Mengen A oder B enthalten sind. Sie bildet das "Gesamt" beider Mengen ohne Duplikate.

Eingabe der Mengen

Werte durch Leerzeichen oder Semikolon getrennt

Werte durch Leerzeichen oder Semikolon getrennt
Ergebnis (A ∪ B)
Vereinigungsmenge:
Alle Elemente aus beiden Mengen (ohne Duplikate)

Vereinigungsmenge Info

Eigenschaften

Vereinigungsmenge A ∪ B:

  • Kommutativ: A ∪ B = B ∪ A
  • Assoziativ: (A ∪ B) ∪ C = A ∪ (B ∪ C)
  • Idempotent: A ∪ A = A
  • A ⊆ (A ∪ B) und B ⊆ (A ∪ B)
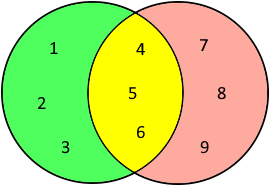
Vereinigungsmenge Venn-Diagramm

Venn-Diagramm der Vereinigungsmenge

Merksatz: "Alle Elemente, die in mindestens einer der beiden Mengen sind."

Inklusions-Exklusions-Prinzip
|A ∪ B| = |A| + |B| - |A ∩ B|

Anzahl Elemente in der Vereinigung

Beispiele
Standard:
{1,2,3} ∪ {2,3,4} = {1,2,3,4}
Disjunkt:
{1,2} ∪ {3,4} = {1,2,3,4}
Teilmenge:
{1,2} ∪ {1,2,3} = {1,2,3}
Verwandte Operationen

→ Schnittmenge
→ Differenzmenge
→ Symmetrische Differenz


Formeln der Vereinigungsmenge

Grunddefinition
\[A \cup B = \{x : x \in A \lor x \in B\}\] Mengenschreibweise
Kommutativgesetz
\[A \cup B = B \cup A\] Reihenfolge beliebig
Assoziativgesetz
\[(A \cup B) \cup C = A \cup (B \cup C)\] Klammerung beliebig
Distributivgesetze
\[A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\] Verteilung über Schnitt
Idempotenz
\[A \cup A = A\] Selbstvereinigung
Neutrale/Absorbierende Elemente
\[A \cup \emptyset = A\] \[A \cup U = U\] Mit leerer Menge und Universalmenge

Detailliertes Rechenbeispiel

Beispiel: A = {1,2,3,4,5,6}, B = {4,5,6,7,8,9}

Gegeben:

  • A = {1, 2, 3, 4, 5, 6}
  • B = {4, 5, 6, 7, 8, 9}

Schritt 1 - Alle Elemente sammeln:

Aus A: 1, 2, 3, 4, 5, 6
Aus B: 4, 5, 6, 7, 8, 9
Gesamt: 1, 2, 3, 4, 5, 6, 7, 8, 9

Schritt 2 - Duplikate entfernen:

A ∪ B = {1,2,3,4,5,6,7,8,9}

Verifikation mit Kardinalität:

|A| = 6, |B| = 6
|A ∩ B| = |{4,5,6}| = 3
|A ∪ B| = 6 + 6 - 3 = 9 ✓

Interpretation: Die Vereinigungsmenge enthält alle verschiedenen Elemente aus beiden Mengen, wobei gemeinsame Elemente nur einmal gezählt werden.

Inklusions-Exklusions-Prinzip

Das fundamentale Prinzip zur Berechnung von Kardinalitäten

Für zwei Mengen:

|A ∪ B| = |A| + |B| - |A ∩ B|

Grund: Gemeinsame Elemente werden sonst doppelt gezählt

Für drei Mengen:

|A ∪ B ∪ C| = |A| + |B| + |C|
- |A ∩ B| - |A ∩ C| - |B ∩ C|
+ |A ∩ B ∩ C|
Praktisches Beispiel

Umfrage in einer Klasse mit 30 Schülern:

Sportarten:
Fußball: 18 Schüler
Basketball: 12 Schüler
Beide Sportarten: 8 Schüler
Berechnung:
Mindestens eine Sportart:
|F ∪ B| = 18 + 12 - 8 = 22 Schüler

Ergebnis: 22 von 30 Schülern treiben mindestens eine der beiden Sportarten.

Gesetze der Vereinigungsmenge

Fundamentale Gesetze der Mengenlehre
Absorptionsgesetz
\[A \cup (A \cap B) = A\]

Absorption des Schnitts

De Morgan 1
\[\overline{A \cup B} = \overline{A} \cap \overline{B}\]

Komplement der Vereinigung

Distributivgesetz
\[A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\]

Verteilung über Schnitt

Monotonie
\[\text{Wenn } A \subseteq B, \text{ dann } A \cup C \subseteq B \cup C\]

Monotonieeigenschaft

Beispiel für Absorptionsgesetz

Gegeben: A = {1,2,3}, B = {2,3,4}

A ∩ B = {2,3}
A ∪ (A ∩ B) = {1,2,3} ∪ {2,3} = {1,2,3} = A ✓

Mathematische Eigenschaften

Grundeigenschaften
  • Obergrenze: A ⊆ (A ∪ B) und B ⊆ (A ∪ B)
  • Kommutativität: A ∪ B = B ∪ A
  • Assoziativität: (A ∪ B) ∪ C = A ∪ (B ∪ C)
  • Idempotenz: A ∪ A = A
Spezielle Eigenschaften
  • Neutrales Element: A ∪ ∅ = A
  • Absorbierendes Element: A ∪ U = U
  • Komplement: A ∪ Ac = U
  • Kleinste obere Schranke: A ∪ B ist die kleinste Menge, die A und B enthält
Wichtige Hinweise

Größenverhältnis: |A ∪ B| ≥ max(|A|, |B|)

Supremum: A ∪ B ist das Supremum (kleinste obere Schranke) von A und B

Praktische Anwendungen

Datenbanken
  • SQL UNION Operationen
  • Datensätze zusammenführen
  • Aggregierte Abfragen
  • Master-Data-Management
Soziale Netzwerke
  • Freundeslisten kombinieren
  • Interessensgruppen
  • Empfehlungssysteme
  • Community-Bildung
Datenanalyse
  • Gesamtpopulationen bilden
  • Kategorien zusammenfassen
  • Umfrage-Auswertungen
  • Marktforschung




Mengen Funktionen

Differenzmenge
Komplement
Schnittmenge
Symmetrische Differenz
Vereinigungsmenge