Symmetrische Differenz

Rechner zur Berechnung der Symmetrischen Differenz mit ausführlichen Formeln und Beispielen

Symmetrische Differenz Rechner

Was wird berechnet?

Die Symmetrische Differenz A ⊕ B (auch A △ B) enthält alle Elemente, die entweder in A oder in B sind, aber nicht in beiden. Sie entspricht dem logischen XOR (exklusives Oder).

Eingabe der Mengen

Werte durch Leerzeichen oder Semikolon getrennt

Werte durch Leerzeichen oder Semikolon getrennt
Ergebnis (A ⊕ B)
Symmetrische Differenz:
Elemente, die nur in einer der beiden Mengen sind

Symmetrische Differenz Info

Eigenschaften

Symmetrische Differenz A ⊕ B:

  • Kommutativ: A ⊕ B = B ⊕ A
  • Assoziativ: (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C)
  • A ⊕ A = ∅ (Selbstauslöschung)
  • A ⊕ ∅ = A (Neutrales Element)
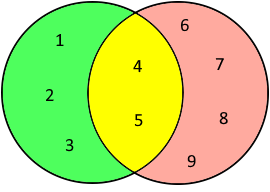
Symmetrische Differenz Venn-Diagramm

Venn-Diagramm der Symmetrischen Differenz

Merksatz: "Entweder A oder B, aber nicht beide gleichzeitig."

XOR-Logik
A B A ⊕ B
000
101
011
110
Beispiele
Standard:
{1,2,3} ⊕ {2,3,4} = {1,4}
Disjunkt:
{1,2} ⊕ {3,4} = {1,2,3,4}
Identisch:
{1,2,3} ⊕ {1,2,3} = ∅
Verwandte Operationen

→ Vereinigungsmenge
→ Schnittmenge
→ Differenzmenge

Formeln der Symmetrischen Differenz

Grunddefinition
\[A \oplus B = (A \setminus B) \cup (B \setminus A)\] Vereinigung der Differenzen
Alternative Definition
\[A \triangle B = (A \cup B) \setminus (A \cap B)\] Vereinigung minus Schnitt
Mengenschreibweise
\[A \oplus B = \{x : (x \in A \land x \notin B) \lor (x \in B \land x \notin A)\}\] Logische Definition
XOR-Darstellung
\[A \oplus B = \{x : x \in A \oplus x \in B\}\] Exklusives Oder
Kommutativgesetz
\[A \oplus B = B \oplus A\] Reihenfolge beliebig
Assoziativgesetz
\[(A \oplus B) \oplus C = A \oplus (B \oplus C)\] Klammerung beliebig

Detailliertes Rechenbeispiel

Beispiel: A = {1,2,3,4,5}, B = {4,5,6,7,8,9}

Gegeben:

  • A = {1, 2, 3, 4, 5}
  • B = {4, 5, 6, 7, 8, 9}

Schritt 1 - Einzelne Differenzen:

A \ B = {1, 2, 3}
B \ A = {6, 7, 8, 9}

Schritt 2 - Vereinigung:

A ⊕ B = {1,2,3,6,7,8,9}

Alternative Berechnung:

A ∪ B = {1,2,3,4,5,6,7,8,9}
A ∩ B = {4,5}
(A ∪ B) \ (A ∩ B) = {1,2,3,6,7,8,9} ✓

Interpretation: Die symmetrische Differenz enthält alle Elemente, die entweder nur in A oder nur in B sind, aber nicht in beiden.

XOR-Logik und Anwendungen

Symmetrische Differenz als XOR-Operation

Digitale Logik:

In der Schaltalgebra entspricht die symmetrische Differenz der XOR-Operation (exklusives Oder). Das Ergebnis ist nur dann "wahr", wenn genau eine der beiden Eingaben "wahr" ist.

Praktisches Beispiel:

Lichter in einem Raum:
Schalter A: {Ein}
Schalter B: {Ein}
XOR-Schaltung: Licht ist AUS (beide Schalter an = aus)

Kryptographie-Anwendung

Einfache Verschlüsselung mit XOR:

Klartext:
{1,0,1,1,0}
Schlüssel:
{1,1,0,1,1}
Chiffrat:
{0,1,1,0,1}

Eigenschaft: Chiffrat ⊕ Schlüssel = Klartext (Selbstinvers)

Algebraische Eigenschaften

Fundamentale Eigenschaften der Symmetrischen Differenz
Selbstauslöschung
\[A \oplus A = \emptyset\]

Menge mit sich selbst ergibt leere Menge

Neutrales Element
\[A \oplus \emptyset = A\]

Leere Menge ist neutrales Element

Selbstinvers
\[A \oplus B \oplus B = A\]

Jede Menge ist ihr eigenes Inverses

Distributivität
\[A \cap (B \oplus C) = (A \cap B) \oplus (A \cap C)\]

Verteilung über Schnitt

Praktisches Beispiel für Selbstinvers

Verschlüsselung und Entschlüsselung:

Klartext: A = {1,3,5}
Schlüssel: B = {2,3,4}
Verschlüsselt: A ⊕ B = {1,2,4,5}
Entschlüsselt: (A ⊕ B) ⊕ B = {1,3,5} = A ✓

Mathematische Eigenschaften

Grundeigenschaften
  • Kommutativität: A ⊕ B = B ⊕ A
  • Assoziativität: (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C)
  • Selbstinvers: A ⊕ A = ∅
  • Neutrales Element: A ⊕ ∅ = A
Spezielle Eigenschaften
  • Gruppenstruktur: (P(U), ⊕) ist abelsche Gruppe
  • Kardinalität: |A ⊕ B| = |A| + |B| - 2|A ∩ B|
  • Disjunkte Mengen: A ⊕ B = A ∪ B wenn A ∩ B = ∅
  • Identische Mengen: A ⊕ A = ∅
Wichtige Hinweise

XOR-Eigenschaft: Symmetrische Differenz entspricht exklusivem Oder

Kryptographie: Basis für viele Verschlüsselungsverfahren

Praktische Anwendungen

Kryptographie
  • XOR-Verschlüsselung
  • One-Time-Pad
  • Stream-Ciphers
  • Diffie-Hellman
Digitaltechnik
  • XOR-Gatter
  • Paritätsprüfung
  • Addierer-Schaltungen
  • Fehlerkorrektur
Datenanalyse
  • Unterschiede finden
  • Exklusive Merkmale
  • Änderungserkennung
  • Differenzanalysen

Mengen Funktionen

Differenzmenge
Komplement
Schnittmenge
Symmetrische Differenz
Vereinigungsmenge