Distanz zwischen zwei Punkten
Berechnung des Abstands zweier Punkte in der Koordinatenebene
Die Distanz zwischen zwei Punkten ist die kürzeste Entfernung zwischen ihnen. Diese wird gemessen als die Länge der geraden Linie, die die beiden Punkte verbindet.
In der Koordinatenebene kann diese Entfernung mit der Abstandsformel (auch Distanzformel genannt) berechnet werden. Sie basiert auf dem Satz des Pythagoras.
Grundkonzept der Distanzberechnung
Wenn zwei Punkte auf einer Koordinatenebene gegeben sind, kann man die gerade Linie zwischen ihnen als Hypotenuse eines rechtwinkligen Dreiecks betrachten.
- Symmetrisch: Der Abstand von A zu B ist gleich dem Abstand von B zu A
- Immer positiv: Die Entfernung kann nie negativ sein
- Null nur identisch: Die Distanz ist nur 0, wenn beide Punkte identisch sind
- Unabhängig von Reihenfolge: Es spielt keine Rolle, welcher Punkt P₁ oder P₂ ist
Die Abstandsformel
Die Distanzformel für zwei Punkte P₁(x₁, y₁) und P₂(x₂, y₂) in der zweidimensionalen Ebene ist:
d: Distanz zwischen den Punkten
(x₁, y₁): Koordinaten des ersten Punktes
(x₂, y₂): Koordinaten des zweiten Punktes
Erweiterung auf 3D
Für Punkte im dreidimensionalen Raum P₁(x₁, y₁, z₁) und P₂(x₂, y₂, z₂) gilt:
Praktisches Berechnungsbeispiel
Berechnen wir die Distanz zwischen den Punkten P₁(0, -2) und P₂(8, 4).
Schritt-für-Schritt Berechnung
Herleitung aus dem Satz des Pythagoras
Die Abstandsformel wird aus dem Satz des Pythagoras hergeleitet. Wenn wir zwei Punkte in der Koordinatenebene haben, können wir ein rechtwinkliges Dreieck konstruieren.
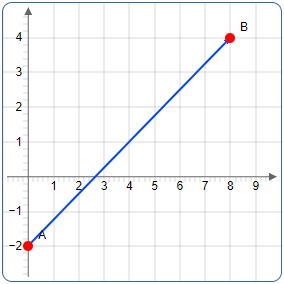
Die beiden Katheten entsprechen den Differenzen der Koordinaten:
Horizontale Kathete
Unterschied in der x-Richtung (horizontal)
Vertikale Kathete
Unterschied in der y-Richtung (vertikal)
Zusammenfassung der Herleitung
Wenn wir die Katheten in den Satz des Pythagoras einsetzen, erhalten wir die Abstandsformel:
Winkelberechnung zur X-Achse
Zusätzlich zur Distanz kann auch der Winkel α zur X-Achse berechnet werden. Dies ist wichtig in Navigation und Ingenieuranwendungen.
Mit Arkustangens
Der Winkel ist der Arkustangens des Verhältnisses der y-Differenz zur x-Differenz.
Alternative: Mit Sinus oder Kosinus
Mit Sinus
d ist die Distanz zwischen den Punkten
Mit Kosinus
d ist die Distanz zwischen den Punkten
Beispiel: Winkelberechnung
Praktische Anwendungen
- GPS und Navigation: Berechnung der Entfernung zwischen geografischen Positionen
- Computergrafik: Entfernungsberechnungen in 2D und 3D-Räumen, Collision Detection
- Vermessungstechnik: Präzise Abstandsmessungen von Vermessungspunkten auf Karten
- Robotik: Bewegungsplanung und Obstacle-Avoidance in autonomen Systemen
- Datenanalyse: Clusteranalyse und räumliche Indizierung in großen Datenmengen
- Geocaching: Bestimmung der Nähe zu Verstecken basierend auf Koordinaten
Tipps und häufige Fehler
- Reihenfolge egal: Abstand(A zu B) = Abstand(B zu A), Ergebnis ist immer gleich
- Negative Koordinaten: Beim Subtrahieren vorsicht mit Vorzeichen (z.B. -2 - 3 = -5)
- 3D-Punkte: Verwenden Sie die erweiterte Formel mit z-Koordinate
- Einheiten merken: Das Ergebnis hat die gleiche Einheit wie die Koordinaten
- Winkelberechnung: Arkustangens gibt Winkel in Radiant oder Grad (je nach Einstellung)
- FALSCH: Differenzen nicht quadrieren | RICHTIG: Beide Differenzen müssen quadriert werden
- FALSCH: Negative Werte unter der Wurzel ignorieren | RICHTIG: Quadrieren macht alle Werte positiv
- FALSCH: Tangens für Division durch Null bei x=x₁ | RICHTIG: In diesem Fall atan2 verwenden oder asin/acos
- FALSCH: Winkel in Grad/Radian verwechseln | RICHTIG: Auf die Einstellung des Rechners achten
Online-Rechner
Berechne schnell und einfach die Distanz zwischen zwei Punkten mit unserem interaktiven Rechner:
|
|