Distance Between Two Points

Calculate the distance between any two points using the distance formula

Overview

The distance between two points is the length of the straight line segment connecting them. This can be calculated using the distance formula, which is derived from the Pythagorean theorem.

Key Principle:

Distance is always positive and independent of the order of the points: the distance from A to B equals the distance from B to A.

The Distance Formula

To find the distance between two points on a coordinate plane, we use the distance formula, derived from the Pythagorean theorem.

Distance Formula:

For two points \(A(x_1, y_1)\) and \(B(x_2, y_2)\):

\(\displaystyle d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)
Formula Components:
  • \(d\) = distance between the two points
  • \(x_1, y_1\) = coordinates of the first point
  • \(x_2, y_2\) = coordinates of the second point

Worked Example

Calculate Distance Between Two Points

Given: Points \(A(0, -2)\) and \(B(8, 4)\)

Find: The distance between points \(A\) and \(B\)

Step 1: Identify the coordinates

\(x_1 = 0, \quad y_1 = -2\)
\(x_2 = 8, \quad y_2 = 4\)

Step 2: Calculate the differences

\(x_2 - x_1 = 8 - 0 = 8\)
\(y_2 - y_1 = 4 - (-2) = 6\)

Step 3: Square the differences

\((x_2 - x_1)^2 = 8^2 = 64\)
\((y_2 - y_1)^2 = 6^2 = 36\)

Step 4: Add the squares

\((x_2 - x_1)^2 + (y_2 - y_1)^2 = 64 + 36 = 100\)

Step 5: Take the square root

\(\displaystyle d = \sqrt{100} = 10\)

Result: The distance between points \(A(0, -2)\) and \(B(8, 4)\) is \(10\) units.

Pythagorean Theorem Connection

The distance formula is derived from the Pythagorean theorem. When we connect two points, we form a right triangle where the distance is the hypotenuse.

Geometric Interpretation

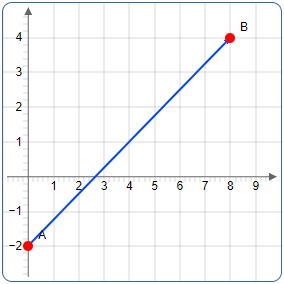
Distance as hypotenuse of right triangle

In the right triangle formed by the two points:

  • Horizontal side (a): \(a = x_2 - x_1\)
  • Vertical side (b): \(b = y_2 - y_1\)
  • Hypotenuse (c): \(c = \sqrt{a^2 + b^2}\) = distance

According to the Pythagorean theorem:

\(\displaystyle c = \sqrt{a^2 + b^2} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)

Angle to the X-Axis

We can also calculate the angle that the line connecting the two points makes with the x-axis using trigonometric functions.

Angle Formulas

Using inverse sine (arcsin):

\(\displaystyle \alpha = \arcsin\left(\frac{y_2 - y_1}{d}\right) = \arcsin\left(\frac{b}{c}\right)\)

Using inverse cosine (arccos):

\(\displaystyle \alpha = \arccos\left(\frac{x_2 - x_1}{d}\right) = \arccos\left(\frac{a}{c}\right)\)
Angle Notation:

\(\alpha\) represents the angle between the line segment and the positive x-axis, measured counterclockwise.

Key Points

  • Distance formula: \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)
  • Distance is derived from the Pythagorean theorem
  • Distance is always positive and symmetric: \(AB = BA\)
  • The order of the points does not matter
  • Distance works with negative coordinates too
  • Angle to x-axis can be found using inverse trigonometric functions

Online Calculator

Use the interactive calculator to quickly compute distances and angles between any two points:

Distance Calculator →


Point coordinates
Midpoint between two points
Distance two points
Slope of a line
Angle definition
















Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?