Punkte im Koordinatensystem
Koordinaten, Darstellung und Eigenschaften von Punkten in der Ebene
Jeder Punkt in einer Ebene kann durch ein Zahlenpaar (x, y) eindeutig beschrieben werden. Diese Zahlen werden Koordinaten des Punktes genannt und bestimmen seine Position im Koordinatensystem.
Das Koordinatensystem besteht aus zwei senkrecht aufeinander stehenden Achsen: der x-Achse (horizontal) und der y-Achse (vertikal). Der Schnittpunkt dieser Achsen wird Ursprung genannt und hat die Koordinaten (0, 0).
Grundkonzept: Koordinaten eines Punktes
Die Koordinaten eines Punktes A werden als geordnetes Paar (x, y) geschrieben:
x: Abstand des Punktes von der y-Achse (Abszisse - horizontal)
y: Abstand des Punktes von der x-Achse (Ordinate - vertikal)
(x, y): Koordinaten des Punktes A
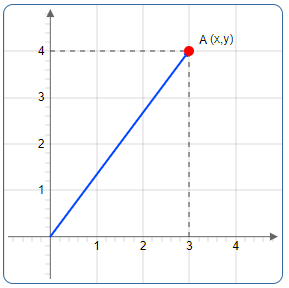
Ein Punkt A mit Koordinaten im Koordinatensystem
- Positive x: Punkte rechts der y-Achse haben positive x-Koordinaten
- Negative x: Punkte links der y-Achse haben negative x-Koordinaten
- Positive y: Punkte oberhalb der x-Achse haben positive y-Koordinaten
- Negative y: Punkte unterhalb der x-Achse haben negative y-Koordinaten
Die vier Quadranten des Koordinatensystems
Die beiden Achsen teilen die Ebene in vier Quadranten auf. Jeder Quadrant hat charakteristische Vorzeichen für die Koordinaten:
I. Quadrant (oben rechts)
Koordinaten: (+ x, + y)
Beispiel: A(3, 4)
Beide Koordinaten sind positiv.
II. Quadrant (oben links)
Koordinaten: (− x, + y)
Beispiel: B(−3, 4)
x negativ, y positiv.
III. Quadrant (unten links)
Koordinaten: (− x, − y)
Beispiel: C(−3, −4)
Beide Koordinaten sind negativ.
IV. Quadrant (unten rechts)
Koordinaten: (+ x, − y)
Beispiel: D(3, −4)
x positiv, y negativ.
Besonderheiten und Eigenschaften
Punkte auf den Achsen
Auf der x-Achse
Form: A(x, 0)
Die y-Koordinate ist immer 0.
Beispiele: (5, 0), (−3, 0), (0, 0)
Auf der y-Achse
Form: A(0, y)
Die x-Koordinate ist immer 0.
Beispiele: (0, 4), (0, −2), (0, 0)
Der Ursprung
Form: O(0, 0)
Schnittpunkt beider Achsen.
Der Nullpunkt des Systems.
Symmetrische Punkte
Es gibt spezielle Beziehungen zwischen Punkten:
- Spiegelung an der x-Achse: A(x, y) wird zu A'(x, −y)
- Spiegelung an der y-Achse: A(x, y) wird zu A'(−x, y)
- Punktspiegelung am Ursprung: A(x, y) wird zu A'(−x, −y)
- Spiegelung an der Geraden y = x: A(x, y) wird zu A'(y, x)
Entfernung zwischen zwei Punkten
Um die Entfernung (Distanz) zwischen zwei Punkten zu berechnen, verwenden wir die Abstandsformel, die auf dem Satz des Pythagoras basiert.
Dies ist die Länge der geraden Linie zwischen den Punkten A(x₁, y₁) und B(x₂, y₂).
Praktisches Beispiel: Distanzberechnung
Finde die Entfernung zwischen den Punkten A(1, 2) und B(4, 5).
Schritt-für-Schritt Berechnung
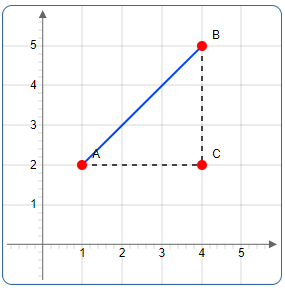
Visualisierung der Distanzberechnung zwischen zwei Punkten mit dem Satz des Pythagoras
Die Strecke AB ist die Hypotenuse eines rechtwinkligen Dreiecks mit den Katheten AC und BC.
Nach dem Satz des Pythagoras gilt: AB² = AC² + BC²
Wobei AC = x₂ − x₁ und BC = y₂ − y₁
Mittelpunkt einer Strecke
Der Mittelpunkt M einer Strecke zwischen zwei Punkten A(x₁, y₁) und B(x₂, y₂) kann einfach berechnet werden, indem man den Durchschnitt der Koordinaten bildet:
Der Mittelpunkt ist der Durchschnitt der Koordinaten beider Punkte.
Beispiel: Mittelpunkt berechnen
Berechnung des Mittelpunkts
Praktische Anwendungen von Koordinaten
- Kartographie und Geografie: Darstellung von geografischen Positionen mit Breiten- und Längengradkoordinaten
- GPS-Navigation: GPS-Systeme verwenden Koordinaten zur Standortbestimmung und Navigation
- Architektur und Bauwesen: Planung von Gebäuden und Grundrissen im Koordinatensystem
- Computergrafik und Spieleentwicklung: Darstellung von Objekten und Kameraperspektiven
- Ingenieurwesen: Technische Zeichnungen, CAD-Systeme und Konstruktionen
- Datenvisualisierung: Darstellung von Daten in Diagrammen, Plots und Grafiken
Tipps und häufige Fehler
- Reihenfolge merken: Erst x (horizontal), dann y (vertikal) - immer in dieser Reihenfolge!
- Vorzeichen beachten: Positive/negative Werte bestimmen den Quadranten eindeutig
- Symmetrien nutzen: Spiegelpunkte haben einfache mathematische Beziehungen
- Visualisieren: Zeichnen Sie die Punkte immer auf, um Fehler zu vermeiden
- Einheiten konsistent halten: Alle Koordinaten sollten die gleiche Einheit haben
- FALSCH: (y, x) statt (x, y) schreiben | RICHTIG: Erst x-Koordinate, dann y-Koordinate
- FALSCH: Vorzeichen ignorieren | RICHTIG: Positive und negative Werte richtig einordnen
- FALSCH: Abstände falsch quadrieren | RICHTIG: In der Abstandsformel beide Differenzen quadrieren
- FALSCH: Quadranten verwechseln | RICHTIG: Die vier Quadranten systematisch unterscheiden
Weitere Ressourcen und verwandte Themen
Weitere Informationen und detaillierte Beispiele zu verwandten Themen:
|
|