Mittelpunkt zwischen zwei Punkten

Berechnung des Mittelpunkts einer Strecke im Koordinatensystem

Diese Seite beschreibt die Berechnung des Mittelpunkts einer Linie zwischen zwei Punkten im Koordinatensystem. Der Mittelpunkt ist der Punkt, der genau in der Mitte einer Strecke liegt und diese in zwei gleich lange Teile teilt.

Die Berechnung des Mittelpunkts ist eine grundlegende geometrische Operation mit vielen praktischen Anwendungen in Mathematik, Physik und Ingenieurwesen.

Grundkonzept des Mittelpunkts

Der Mittelpunkt einer Strecke zwischen zwei Punkten ist der Punkt, der den gleichen Abstand zu beiden Endpunkten hat. Um den Mittelpunkt zu berechnen, bildet man einfach den Durchschnitt der Koordinaten beider Punkte.

Mittelpunktformel:
M = ((x₁ + x₂)/2, (y₁ + y₂)/2)

M: Mittelpunkt der Strecke
A(x₁, y₁): Erster Punkt
B(x₂, y₂): Zweiter Punkt

Wichtige Eigenschaften des Mittelpunkts:
  • Eindeutig: Es gibt genau einen Mittelpunkt zwischen zwei Punkten
  • Durchschnitt: Die Koordinaten sind der Durchschnitt beider Punkte
  • Symmetrisch: Der Mittelpunkt hat gleichen Abstand zu beiden Endpunkten
  • Auf der Strecke: Der Mittelpunkt liegt immer auf der Verbindungslinie

Praktisches Beispiel 1: Ganzzahlige Koordinaten

Finde den Mittelpunkt zwischen den Punkten A(2, 3) und B(4, 5).

Schritt-für-Schritt Berechnung
Gegeben: A(2, 3) und B(4, 5)
Formel: M = ((x₁ + x₂)/2, (y₁ + y₂)/2)
x-Koordinate des Mittelpunkts: (2 + 4)/2 = 6/2 = 3
y-Koordinate des Mittelpunkts: (3 + 5)/2 = 8/2 = 4
Resultat: Der Mittelpunkt M hat die Koordinaten (3, 4)
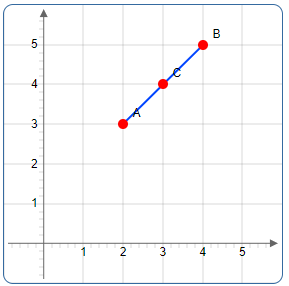
Mittelpunkt Beispiel

Visualisierung des Mittelpunkts zwischen A(2, 3) und B(4, 5)

Praktisches Beispiel 2: Mit negativen Koordinaten

Finde den Mittelpunkt zwischen den Punkten A(−3, 2) und B(5, −4).

Berechnung mit negativen Koordinaten
Gegeben: A(−3, 2) und B(5, −4)
Formel: M = ((x₁ + x₂)/2, (y₁ + y₂)/2)
x-Koordinate: (−3 + 5)/2 = 2/2 = 1
y-Koordinate: (2 + (−4))/2 = −2/2 = −1
Resultat: Der Mittelpunkt M ist (1, −1)
Hinweis zu negativen Zahlen:

Bei negativen Koordinaten vorsichtig mit den Vorzeichen umgehen. Die Formel funktioniert genauso, auch wenn Koordinaten negativ sind.

Praktisches Beispiel 3: Mit Dezimalkoordinaten

Finde den Mittelpunkt zwischen den Punkten A(1.5, 2.5) und B(3.5, 4.5).

Berechnung mit Dezimalzahlen
Gegeben: A(1.5, 2.5) und B(3.5, 4.5)
x-Koordinate: (1.5 + 3.5)/2 = 5/2 = 2.5
y-Koordinate: (2.5 + 4.5)/2 = 7/2 = 3.5
Resultat: Der Mittelpunkt M ist (2.5, 3.5)

Mittelpunkt im dreidimensionalen Raum

Die Mittelpunktformel kann auch auf den dreidimensionalen Raum erweitert werden, indem man einfach die z-Koordinate hinzufügt:

Mittelpunktformel (3D):
M = ((x₁ + x₂)/2, (y₁ + y₂)/2, (z₁ + z₂)/2)

Für Punkte im dreidimensionalen Raum wird die Formel einfach um die z-Koordinate erweitert.

Beispiel 3D-Mittelpunkt

Mittelpunkt im 3D-Raum
Gegeben: A(1, 2, 3) und B(5, 6, 7)
x-Koordinate: (1 + 5)/2 = 3
y-Koordinate: (2 + 6)/2 = 4
z-Koordinate: (3 + 7)/2 = 5
Resultat: Der Mittelpunkt M ist (3, 4, 5)

Herleitung der Mittelpunktformel

Die Mittelpunktformel kann geometrisch verstanden werden. Der Mittelpunkt M der Strecke AB hat die Eigenschaft, dass die Distanz von A zu M gleich der Distanz von M zu B ist.

Mathematische Herleitung

Wenn wir fordern, dass M in der Mitte liegt, bedeutet das:

AM = MB
M − A = B − M
2M = A + B
M = (A + B)/2

Dies zeigt, dass der Mittelpunkt tatsächlich der Durchschnitt (der Mittelwert) der beiden Endpunkte ist.

Besondere Eigenschaften und Beziehungen

Symmetrie

Der Mittelpunkt M einer Strecke AB hat eine wichtige Symmetrieeigenschaft:

Abstandssymmetrie

d(A, M) = d(M, B)

Der Abstand von A zum Mittelpunkt ist gleich dem Abstand vom Mittelpunkt zu B.

Spiegelung

Der Mittelpunkt ist das Zentrum der Spiegelung für die beiden Punkte A und B.

Mittelpunkt und Distanz

Beziehung zur Distanzformel:

Die Länge der halben Strecke ist die Hälfte der Distanz zwischen A und B:
d(A, M) = d(B, M) = d(A, B) / 2

Praktische Anwendungen des Mittelpunkts

  • Geometrische Konstruktionen: Teilen von Strecken in gleiche Teile
  • Architektur: Symmetrische Anordnung von Elementen
  • Navigation: Berechnung von Treffpunkten oder Rastplätzen
  • Computergrafik: Berechnung von Mittelpunkten für Skalierung und Rotation
  • Physik: Schwerpunkte und Massenmittelpunkte von Objekten
  • Wirtschaft: Mittelwertberechnungen und Durchschnittswerte

Tipps und häufige Fehler

Hilfreiche Tipps:
  • Durchschnitt bilden: Der Mittelpunkt ist einfach der Durchschnitt der Koordinaten
  • Beide Achsen: Denken Sie daran, sowohl x als auch y Koordinaten zu berechnen
  • Negative Werte: Mit negativen Koordinaten normal umgehen, die Formel funktioniert gleich
  • Symmetrie merken: Der Mittelpunkt teilt die Strecke in zwei gleich lange Teile
  • Verifikation: Überprüfen Sie, ob der Mittelpunkt zwischen den beiden Punkten liegt
Häufige Fehler:
  • FALSCH: Nur eine Koordinate durchschnittlich | RICHTIG: Beide x und y durchschnittlich berechnen
  • FALSCH: Division durch 2 vergessen | RICHTIG: Immer (x₁ + x₂)/2 rechnen, nicht nur (x₁ + x₂)
  • FALSCH: Mit negativen Zahlen falsch rechnen | RICHTIG: Sorgfältig mit Vorzeichen umgehen
  • FALSCH: Mittelpunkt nicht auf Strecke liegen | RICHTIG: Der Mittelpunkt liegt immer auf der Verbindungslinie

Vergleich: 2D vs. 3D Mittelpunkte

Eigenschaft 2D-Mittelpunkt 3D-Mittelpunkt
Dimension 2 Koordinaten (x, y) 3 Koordinaten (x, y, z)
Formel M = ((x₁+x₂)/2, (y₁+y₂)/2) M = ((x₁+x₂)/2, (y₁+y₂)/2, (z₁+z₂)/2)
Anwendung Ebene Geometrie Raumgeometrie
Beispiele Kartografie, Architektur CAD, 3D-Grafik, Physik

Online-Rechner

Um den Mittelpunkt schnell zu berechnen, können Sie unseren Online-Rechner verwenden oder die Formel manuell anwenden.

Weitere Ressourcen

Weitere Informationen zu verwandten Themen:



Punkte im Koordinatensystem
Mittelpunkt zwischen zwei Punkten im Koordinatensystem
Distanz zwischen zwei Punkten
Steigung-einer-Geraden (Gradient)
Winkel Definition


























Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?