Midpoint Between Two Points

Calculate the midpoint coordinates of a line segment between two points

Overview

The midpoint is the point that lies exactly halfway between two given points on a line segment. It divides the segment into two equal parts.

Key Concept:

The midpoint can be calculated by finding the average of the x-coordinates and the average of the y-coordinates of the two endpoints.

The Midpoint Formula

To find the midpoint of a line segment between two points, we use a simple formula based on averaging coordinates.

General Midpoint Formula

For two points \(A(x_1, y_1)\) and \(B(x_2, y_2)\), the midpoint \(C\) has coordinates:

\(\displaystyle C = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)\)
How it Works:
  • x-coordinate of midpoint: Average of the two x-coordinates
  • y-coordinate of midpoint: Average of the two y-coordinates

Worked Example

Find the Midpoint of Two Points

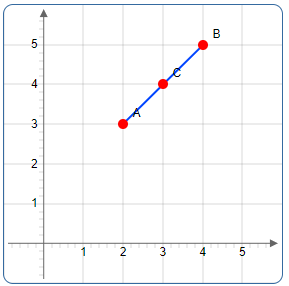
Given: Point \(A(2, 3)\) and Point \(B(4, 5)\)

Find: The midpoint \(C\) of the line segment \(AB\)

Visual Representation

Midpoint between two points

Step 1: Calculate the x-coordinate of the midpoint

\(\displaystyle x_C = \frac{x_1 + x_2}{2} = \frac{2 + 4}{2} = \frac{6}{2} = 3\)

Step 2: Calculate the y-coordinate of the midpoint

\(\displaystyle y_C = \frac{y_1 + y_2}{2} = \frac{3 + 5}{2} = \frac{8}{2} = 4\)

Step 3: Write the midpoint coordinates

\(\displaystyle C = (3, 4)\)

Result: The midpoint between \(A(2, 3)\) and \(B(4, 5)\) is \(C(3, 4)\). This point lies exactly halfway along the line segment connecting the two points.

Verification

We can verify our answer by checking that the distances from the midpoint to each endpoint are equal.

Verify the Midpoint

Distance from \(C(3,4)\) to \(A(2,3)\):

\(\displaystyle CA = \sqrt{(3-2)^2 + (4-3)^2} = \sqrt{1 + 1} = \sqrt{2} \approx 1.414\)

Distance from \(C(3,4)\) to \(B(4,5)\):

\(\displaystyle CB = \sqrt{(4-3)^2 + (5-4)^2} = \sqrt{1 + 1} = \sqrt{2} \approx 1.414\)

Verification: Since \(CA = CB\), point \(C\) is indeed the midpoint. ✓

Properties of the Midpoint

Symmetry
The midpoint divides the segment into two equal parts
Equal Distance
Distance from midpoint to each endpoint is equal
Average Position
The midpoint is the average of both endpoints

Key Points

  • Midpoint formula: \(C = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)\)
  • The midpoint lies exactly halfway between the two endpoints
  • Both x and y coordinates are averages of the respective endpoint coordinates
  • Distance from midpoint to each endpoint is always equal
  • Works for all points in the coordinate system (including negative coordinates)
  • The midpoint is unique for any two distinct points


Point coordinates
Midpoint between two points
Distance two points
Slope of a line
Angle definition












Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?