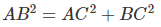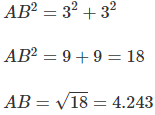Points in the coordinate system
Description and formulas for points in the coordinate system
Introduction
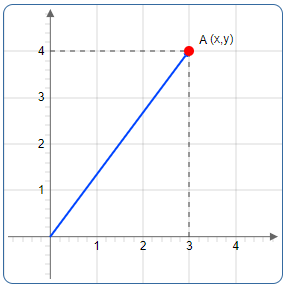
Any point can be described by a pair of numbers \((x, y)\). The numbers are the distance of A from the y axis \((x)\) , and from the x axis \((y)\). The pair \((x, y)\) are called the coordinates of the point A. Any points to the left of the y-axis will have a negative x coordinate. Any points below the x axis, will have a negative y coordinate.
The distance between 2 points
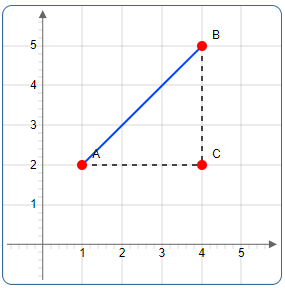
Find the distance between two points \(A (1,2)\) and \(B (4,5)\).
To find the length \(AB\) we use Pythagoras’ Theorem. \(AB\) is the hypotenuse of an appropriate right-angled triangle \(ABC\). This means that \(C\) must be the point \((4,2)\)
The distance \(AC\) is \(4 − 1 = 3\)
The distance \(BC\) is \(5 − 2 = 3\)
According to Pythagoras Theorem
Substitute the values for \(AC\) and \(BC\)
The distance between \(A\) and \(B\) is \(4.243\).
You can derive a general formula to use instead
More examples you can find here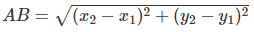
|
|