Trapez Diagonale f mit Winkel berechnen
Rechner und Formeln zur Trapez Diagonalen f über Seitenlängen und Winkel α
Trapez Diagonale f (Winkel α-Methode)
Winkel-basierte Berechnung der zweiten Diagonale
Die Diagonale f kann bei bekannten Seitenlängen a und d und dem Winkel α direkt mit dem Cosinussatz berechnet werden, ohne die Höhe zu benötigen.
Trapez mit Winkel α
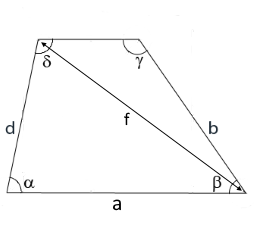
Das Diagramm zeigt ein Trapez mit den Seiten a und d und dem Winkel α.
Die Diagonale f wird über den Cosinussatz berechnet.
|
|
Winkel-basierte Berechnung der Diagonale f
Die zweite Diagonale f kann analog zur ersten Diagonale e über Winkel berechnet werden:
- Andere Seitenkombination: Nutzt Seiten a und d statt a und b
- Winkel α: Eingeschlossener Winkel zwischen a und d
- Cosinussatz: Direkter Ansatz ohne Höhenberechnung
- Flexibilität: Funktioniert bei verschiedenen Trapez-Formen
- Ergänzung: Alternative zur höhen-basierten Berechnung
- Anwendung: Besonders nützlich in der Vermessung
Der Winkel α für Diagonale f
Der Winkel α zwischen den Seiten a und d bestimmt die Länge der Diagonale f:
Definition
- Winkel zwischen den Seiten a und d
- Meist anders als Winkel β für Diagonale e
- Gemessen in Grad (°) oder Radiant
- Bestimmt die Geometrie des Trapezes
Einfluss auf Diagonale f
- Cosinus des Winkels bestimmt die Länge
- Bei α=90° entspricht es dem Pythagoras
- Spitze Winkel ergeben längere Diagonalen
- Stumpfe Winkel verkürzen die Diagonale
Cosinussatz für Diagonale f
Der Cosinussatz ermöglicht die direkte Berechnung der Diagonale f:
Formel
Analog zur Formel für Diagonale e
Anwendung
- Gleiche mathematische Basis wie bei e
- Andere Seitenkombination (a, d statt a, b)
- Verschiedener Winkel (α statt β)
- Meist andere Diagonalenlänge
Formeln zur winkel-basierten Berechnung der Diagonale f
Hauptformel: Cosinussatz für Diagonale f
Diagonale f aus Seiten a, d und dem eingeschlossenen Winkel α
Winkel in Radiant
Umrechnung von Grad in Radiant
Spezialfall α = 90°
Reduziert sich zum Pythagoras
Alternative mit Seiten c, b
Mit anderen Seiten und Winkel γ
Vergleich mit Diagonale e
Analog mit Seiten a, b und Winkel β
Höhen-basierte Alternative
\(x = \sqrt{d^2 - h^2}\)
Horizontale Projektion der Seite d
\(f = \sqrt{(a-x)^2 + h^2}\)
Pythagoras im rechtwinkligen Dreieck
Rechenbeispiel
Gegeben
Gesucht: Diagonale f
1. Cosinus berechnen
Bekannter trigonometrischer Wert
2. Werte einsetzen
Cosinussatz anwenden
3. Endergebnis
Die Diagonale f hat eine Länge von etwa 5.57 Einheiten
4. Vergleich mit Diagonale e
Berechnung der Diagonale e (angenommen b = 5, β = 60°):
\(e^2 = 6^2 + 5^2 - 2 \cdot 6 \cdot 5 \cdot \cos(60°) = 36 + 25 - 30 = 31\)
\(e = \sqrt{31} \approx 5.57\)
In diesem Beispiel sind beide Diagonalen gleich lang, da d = b und α = β.
Plausibilitätsprüfung: Bei α=60° ist cos(60°) = 0.5 > 0, somit f < √(a²+d²) = √61 ≈ 7.81 ✓
Winkel-basierte Berechnung der Diagonale f in Theorie und Praxis
Die winkel-basierte Berechnung der Diagonale f vervollständigt das geometrische Verständnis von Trapez-Diagonalen. Als zweite Diagonale ergänzt sie die Diagonale e und ermöglicht zusammen mit ihr eine vollständige Charakterisierung der inneren Trapez-Struktur. Der Cosinussatz bietet auch hier einen eleganten direkten Berechnungsweg.
Die Diagonale f - Eigenschaften und Bedeutung
Die Diagonale f ist die zweite Hauptdiagonale des Trapezes und unterscheidet sich von e:
- Alternative Verbindung: Verbindet die anderen beiden nicht benachbarten Eckpunkte
- Verschiedene Seitenbasis: Nutzt die Seiten a und d statt a und b
- Anderer Winkel: Der Winkel α zwischen a und d ist meist verschieden von β
- Unterschiedliche Länge: Bei allgemeinen Trapezen meist f ≠ e
- Gleichheit nur bei Symmetrie: f = e nur bei gleichschenkligen Trapezen
Der Winkel α im Kontext
Der Winkel α spielt eine zentrale Rolle bei der Charakterisierung des Trapezes:
Geometrische Bedeutung
Der Winkel α zwischen den Seiten a und d bestimmt zusammen mit den Seitenlängen die Form des Trapezes und die Länge der Diagonale f.
Beziehung zu anderen Winkeln
In einem Trapez sind die Winkel durch die Parallelität der Grundseiten miteinander verknüpft. Die Summe aller Innenwinkel beträgt 360°.
Praktische Messbarkeit
Winkel sind oft einfacher zu messen als Höhen, besonders bei großen Strukturen oder in der Vermessung.
Konstruktive Vorgabe
In der Praxis werden Winkel häufig als Designparameter vorgegeben, aus denen dann andere Größen abgeleitet werden.
Praktische Anwendungen
Die winkel-basierte Berechnung der Diagonale f findet in vielen Bereichen Anwendung:
Struktureller Ingenieurbau
- Fachwerke: Beide Diagonalen für maximale Stabilität
- Brückenbau: Kreuzweise Verstrebung
- Stahlbau: Redundante Tragstrukturen
- Hochbau: Gebäudeaussteifung
Vermessung und Kartografie
- Triangulation: Beide Diagonalen für Genauigkeit
- Flächenvermessung: Vollständige Trapez-Charakterisierung
- GPS-Messungen: Redundante Bestimmung
- Katastervermessung: Präzise Grenzbestimmung
Design und Architektur
- Moderne Architektur: Asymmetrische Gestaltung
- Dachkonstruktionen: Verschiedene Sparrenrichtungen
- Innenarchitektur: Dynamische Raumaufteilung
- Landschaftsarchitektur: Komplexe Wegeführung
Maschinenbau und Technik
- Getriebetechnik: Mehrrichtungs-Kraftübertragung
- Robotik: Komplexe Gelenkkinematik
- Fahrzeugbau: Chassisversteifung
- Optik: Prismengeometrie
Zusammenfassung
Die winkel-basierte Berechnung der Diagonale f vervollständigt das geometrische Verständnis von Trapezen. Zusammen mit der Diagonale e ermöglicht sie eine vollständige Charakterisierung der Trapez-Geometrie. Der Cosinussatz bietet einen eleganten und direkten Berechnungsweg, der besonders in der modernen Technik und beim computergestützten Design von großer Bedeutung ist.
|
|
|
|