Calculate Triangle Medians
Calculate the medians and centroid of a triangle
Triangle Median Calculator
Medians and Centroid
Medians connect vertices with midpoints of opposite sides. Their intersection (centroid) is the balance point of the triangle.
Medians in Triangle
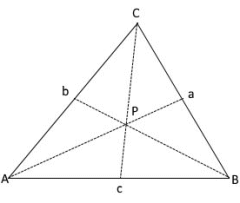
The three medians (red) connect vertices with midpoints of opposite sides.
The centroid P divides each median in a 2:1 ratio.
|
|
What are Medians?
Medians are fundamental lines in every triangle:
- Definition: Connects vertex with midpoint of opposite side
- Count: Every triangle has exactly three medians
- Division: Each median divides the triangle into two equal areas
- Intersection: All three medians meet at the centroid
- Ratio: Centroid divides each median in a 2:1 ratio
- Balance: The centroid is the balance point of the triangle
The Centroid
The centroid is the remarkable intersection point of all three medians:
Unique Intersection Point
- All three medians meet at one point
- Always lies inside the triangle
- Independent of triangle shape
- Geometric center of the triangle
2:1 Division Ratio
- Divides each median into two segments
- From vertex: 2/3 of median length
- To opposite side: 1/3 of median length
- Constant ratio for all triangles
Balance and Physical Properties
The centroid has special physical significance:
Balance Point
- Triangle balances perfectly on this point
- Center of mass with uniform density
- Equilibrium in all directions
- Minimum moment of inertia point
Area Division
- Each median divides triangle into two equal areas
- Centroid divides triangle into three equal sub-areas
- All divisions through centroid are equal in area
- Optimal division for many applications
Special Properties of Medians
Medians have unique mathematical properties:
Area Division
- Divides triangle into two equal areas
- Both sub-areas = A/2
- Independent of triangle shape
Length Relationship
- Length depends on all three sides
- Apollonius theorem applicable
- Connection to side lengths
Centroid
- Always inside the triangle
- 2:1 division ratio constant
- Coordinates = average of vertices
Formulas for Medians
Median mₐ (from A)
Median from vertex A to side a
Median m_b (from B)
Median from vertex B to side b
Median m_c (from C)
Median from vertex C to side c
Apollonius Theorem
The formulas for medians are based on the Apollonius theorem, which describes the relationship between side lengths and medians:
This theorem shows how the length of a median depends on all three side lengths.
Centroid Coordinates
If the vertices are known: A(x₁,y₁), B(x₂,y₂), C(x₃,y₃), then the centroid coordinates are:
The centroid is the average of all vertex coordinates.
Notation and Symbols
- a, b, c: Side lengths of the triangle
- mₐ, m_b, m_c: Medians
- S (or G): Centroid
- A, B, C: Vertices of the triangle
- 2:1: Division ratio at centroid
- Mₐ, M_b, M_c: Side midpoints
- Median: Line from vertex to side midpoint
- Centroid: Center of mass point
Calculation Example
Given
Right triangle (3-4-5)
1. Calculate Median mₐ
Median from A to side a
2. Calculate Median m_b
Median from B to side b
3. Calculate Median m_c
Median from C to hypotenuse
Special Property
In a right triangle, the median to the hypotenuse is exactly half the length of the hypotenuse: m_c = c/2 = 5/2 = 2.5 ✓
Triangle Medians in Mathematics and Applications
Triangle medians belong to the most fundamental lines of triangle geometry. They combine geometric elegance with practical applicability and show remarkable mathematical properties that extend far beyond pure geometry.
Definition and Basic Properties
A median is defined as the line connecting a vertex with the midpoint of the opposite side:
- Unique definition: Each vertex determines exactly one median
- Three medians: Every triangle has exactly three medians
- Area division: Each median divides the triangle into two equal areas
- Interior position: Medians always run completely inside the triangle
- Universality: Exist in every triangle, regardless of shape or size
The Centroid - A Special Point
The intersection point of all three medians has extraordinary properties:
Geometric Properties
The centroid always lies inside the triangle and divides each median in a 2:1 ratio, with the longer segment pointing toward the vertex.
Coordinate Calculation
The coordinates of the centroid are simply the arithmetic mean of the vertex coordinates.
Physical Significance
With uniform mass distribution, the centroid is the center of mass and balance point of the triangle.
Minimal Property
The centroid minimizes the sum of squared distances to all vertices.
The Apollonius Theorem
The lengths of medians are described by the elegant Apollonius theorem:
Mathematical Formulation
For median mₐ: 4m²ₐ = 2b² + 2c² - a². This relationship connects all side lengths with the median length.
Derivation
The theorem can be elegantly derived via vector calculus or the law of cosines.
Application
Enables direct calculation of median lengths from the three side lengths without angle calculations.
Generalization
The theorem can be extended to higher dimensions and other geometric objects.
Practical Applications
Medians and the centroid have diverse practical applications:
- Engineering: Center of gravity determination for load calculations, structural planning
- Computer graphics: Triangulation, mesh generation, centroid-based algorithms
- Robotics: Balance control, path planning, center of mass calculation
- Physics: Rotational dynamics, moments of inertia, stability of moving objects
- Cartography: Area centroids of regions, geographic centers
- Architecture: Static calculations, material distribution, weight balance
Relationships to Other Triangle Lines
Altitudes
Unlike altitudes, medians do not stand perpendicular to the sides, but have other remarkable properties.
Angle Bisectors
Only in equilateral triangles do medians and angle bisectors coincide.
Perpendicular Bisectors
Perpendicular bisectors and medians are completely different lines with different properties.
Medians of the Midlines
The connecting lines of the side midpoints form the medial triangle with special properties.
Special Cases and Particular Triangles
In different triangle types, medians show special properties:
- Equilateral triangle: All medians are equal length and coincide with altitudes, angle bisectors, and perpendicular bisectors
- Isosceles triangle: The median to the base coincides with the altitude
- Right triangle: The median to the hypotenuse is exactly half the length of the hypotenuse
- Obtuse triangle: All medians remain inside the triangle, although one altitude lies outside
Historical Development
The study of medians has a long history:
Antiquity
The basic properties of medians were already known in ancient Greece.
Apollonius of Perga
Developed around 200 BC the theorem about median lengths named after him.
Modern Mathematics
Vector and analytical treatment enabled deeper insights into the properties.
Application Areas
Development of new applications in computer science, physics, and engineering.
Algorithms and Calculation
The calculation of medians is done systematically:
- Input: The three side lengths a, b, c of the triangle
- Validation: Check triangle inequality
- Apply Apollonius theorem: For each of the three medians
- Numerical stability: Handle rounding errors for extreme ratios
- Output: The three median lengths with desired precision
Summary
Triangle medians are fundamental geometric elements that combine elegant mathematical properties with practical applicability. The centroid as their common intersection point is a point of extraordinary geometric and physical significance. The Apollonius theorem provides an elegant method for calculating median lengths and shows the deep connection between different geometric properties of a triangle.
|
|
|
|
Bisector of a triangle • Equilateral triangle • Right triangles • Right triangle, given 1 side and 1 angle • Isosceles right triangles • Isosceles triangles • Triangle area, given 2 sides and 1 anglee • Triangle area, given 1 side and 2 angles • Triangle, Incircle, given 3 sides • Area of a triangle given base and height • Triangle vertices, 3 x/y points •