Calculate Triangle Area
Calculate triangle area from three sides using Heron's formula
Heron's Formula Calculator
Heron's Area Formula
Heron's formula calculates the area from three side lengths without angles or heights needed.
Visualization
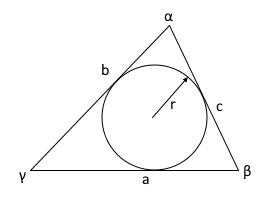
The diagram shows a triangle with all three sides a, b, c and the incircle.
Heron's formula calculates the area from side lengths only.
Note Triangle Inequality
Each side must be smaller than the sum of the other two: a < b + c, b < a + c, c < a + b
|
|
What is Heron's Formula?
Heron's formula is one of the most elegant methods in geometry:
- Only side lengths: No angles or heights required
- Universal: Works for all triangle types
- Complete: Determines all other triangle properties
- Historical: Named after Hero of Alexandria (1st century AD)
- Applications: Surveying, CAD, material calculation
- Foundation: For further calculations like incircle and angles
The Triangle's Incircle
The incircle is the largest circle that fits completely inside the triangle:
Incircle Properties
- Touches all three sides of the triangle
- Center lies at intersection of angle bisectors
- Radius r = Area / Semi-perimeter
- Optimal use of triangle's interior space
Calculation via Heron
- Area A via Heron's formula
- Semi-perimeter s = (a + b + c) / 2
- Incircle radius r = A / s
- Incircle area = π × r²
Understanding Calculation Steps
The Heron calculation follows systematic steps:
1. Validation
Check triangle inequality for all three sides
2. Semi-perimeter
s = (a + b + c) / 2 as foundation for all further calculations
3. Heron's Formula
A = √[s(s-a)(s-b)(s-c)] for area calculation
4. Further Values
Angles via law of cosines, heights and incircle properties
Heron's Formula and Further Calculations
The Classic Heron's Formula
Alternative Heron's Formulas
Incircle Calculations
Angle α
Angle β
Angle γ
Calculate Height
Height to side a
Circumcircle Radius
Radius of the circumcircle
Symbols and Notation
- A: Area of the triangle
- a, b, c: Side lengths of the triangle
- s: Semi-perimeter (a+b+c)/2
- α, β, γ: Interior angles of the triangle
- r: Incircle radius
- R: Circumcircle radius
- h: Height of the triangle
- √: Square root (characteristic of Heron)
Calculation Example
Given
1. Semi-perimeter
Semi-perimeter s = 6
2. Heron's Formula
The area is 6 square units
3. Incircle
Incircle radius r = 1, area = π ≈ 3.14
4. Special Property
This is a right triangle!
3² + 4² = 9 + 16 = 25 = 5²
Check: A = ½ × 3 × 4 = 6 ✓
5. Angles
β ≈ 53.13°
γ ≈ 36.87°
Heron's Formula in Mathematics and Applications
Heron's formula (also called Hero's area formula) is one of the most remarkable discoveries of ancient mathematics. It enables the calculation of triangle area exclusively from the three side lengths, without requiring angles, heights, or other geometric constructions.
Historical Background
The formula bears the name of the Alexandrian mathematician Hero (ca. 10-70 AD):
- Hero of Alexandria: Greek mathematician and engineer of antiquity
- Documentation: First systematic presentation in "Metrica" (ca. 60 AD)
- Earlier origins: Possibly already known to Archimedes (287-212 BC)
- Chinese mathematics: Similar formulas in "Liu Hui" (3rd century AD)
- Modern significance: Fundamental building block of analytical geometry
Mathematical Structure and Elegance
Symmetric Form
The formula A = √[s(s-a)(s-b)(s-c)] shows perfect symmetry with respect to all three side lengths. Each side is treated equally.
Square Root Character
The characteristic root makes the formula unique among area formulas and gives it its special mathematical elegance.
Semi-perimeter as Key
The semi-perimeter s = (a+b+c)/2 is the central parameter that encodes all geometric properties of the triangle.
Product Form
The product s(s-a)(s-b)(s-c) contains all information about the shape and size of the triangle in compact form.
Geometric Interpretation
The terms (s-a), (s-b), (s-c) have an intuitive geometric meaning:
- s-a: "Excess" of semi-perimeter over side a
- s-b: "Excess" of semi-perimeter over side b
- s-c: "Excess" of semi-perimeter over side c
- Product: Encodes the "balance" of side ratios
Practical Applications
Heron's formula finds wide application in various fields:
- Land surveying: Area calculation of irregular properties
- Construction planning: Material calculation for triangular constructions
- CAD software: Automatic area calculation in technical drawings
- Geodesy: Triangulation and terrain surveying
- Computer graphics: Polygon area calculation and mesh analysis
- Physics: Cross-section calculations and materials science
Related Calculations
Heron's formula is the starting point for many other triangle calculations:
Incircle Properties
- Incircle radius: r = A/s
- Incircle area: π × r²
- Tangent points on sides
- Optimal circle inscription
Other Properties
- Heights: h = 2A/side
- Angles via law of cosines
- Circumcircle radius: R = abc/(4A)
- Centroid and other centers
Alternative Formulations
Heron's formula can be presented in various mathematically equivalent forms:
- Classic form: A = √[s(s-a)(s-b)(s-c)]
- Extended form: A = ¼√[(a+b+c)(-a+b+c)(a-b+c)(a+b-c)]
- Determinant form: A = ¼√[4a²b² - (a²+b²-c²)²]
- Brahmagupta generalization: For quadrilaterals (for cyclic quadrilaterals)
Numerical Aspects
In practical application, various numerical considerations are important:
- Triangle inequality: Mandatory check before calculation
- Numerical stability: Problems with very "thin" triangles
- Rounding errors: Amplification with unfavorable side ratios
- Alternative algorithms: Kahan formula for better numerical properties
Generalizations and Extensions
Higher Dimensions
Generalizations for tetrahedra (Cayley-Menger determinant) and higher-dimensional simplices in analytical geometry.
Spherical Geometry
Adaptations for triangles on sphere surfaces with correspondingly modified trigonometric relationships.
Hyperbolic Geometry
Variants for non-Euclidean geometries with adapted distance concepts and angle definitions.
Computer Algebra
Symbolic calculations and exact arithmetic for theoretical investigations and proofs.
Modern Significance
In today's mathematics and technology, Heron's formula remains highly relevant:
- Algorithmic geometry: Building block for computational geometry
- Finite elements: Area calculation in numerical simulations
- Computer vision: Object recognition and 3D reconstruction
- Robotics: Path planning and collision detection
- Game development: Physics engines and collision detection
Summary
Heron's formula is a masterpiece of ancient mathematics that has lost none of its elegance and practical significance to this day. It connects mathematical beauty with practical applicability and forms a bridge between classical geometry and modern computer-aided calculations. Its simplicity in application combined with mathematical depth makes it an indispensable tool for mathematicians, engineers, and scientists of all disciplines.
|
|
|
|
Bisector of a triangle • Equilateral triangle • Right triangles • Right triangle, given 1 side and 1 angle • Isosceles right triangles • Isosceles triangles • Triangle area, given 2 sides and 1 anglee • Triangle area, given 1 side and 2 angles • Triangle, Incircle, given 3 sides • Area of a triangle given base and height • Triangle vertices, 3 x/y points •