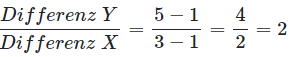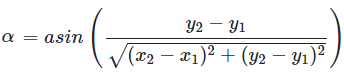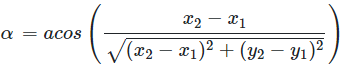Slope of a straight line

The slope of a line is called the gradient. It is a measure of how steep the line is. A line with a large gradient will be steep; a line with a small gradient will be relatively flat; and a line with a zero gradient will be horizontal.

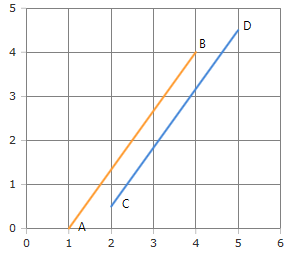
The next figure shows three line segments. The line segment \(AD\) is steeper than the line segment \(AC\). \(AC\) is steeper than \(AB\), which is horizontal. The slope is quantified mathematically, by measuring the relative changes in \(x\) and \(y\), as we move from the beginning to the end of the line segment

"

For the segment \(AD\), \(y\) changes from \(1\) to \(5\), \(x\) changes from \(1\) to \(3\). So the change in \(y\) is \(4\), and the change in \(x\) is \(2\). The relative change, the gradient of the line segment, is

Lines that are steeper have a larger gradient than lines that are less steep. The gradient of the horizontal lines is zero.

The gradient of a line is equal to the tangent of the angle that the line makes with the horizontal. This is also the tangent of the angle the line makes with the x-axis.

Parallel lines

Apply knowledge of gradients to the case of parallel lines. If line \(1\) and line \(2\) are two parallel lines, then the angles \(θ1\) and \(θ2\) they make with the x-axis are equal. Therefore, parallel lines must have the same gradient

The next figure shows two parallel lines with the gradient \(m = 1.333\).

Calculate angle to the X axis