Vector Addition
Formula and examples for adding vectors
The following article describes vector additions using vectors of two or three elements. Basically, vectors can contain any number of elements.
Vectors can be added by adding the individual elements. However, vectors can only be added if they have the same number of dimensions and the same orientation (columns or row-oriented).
The following vectors can be added. They have the same number of elements and orientation.
\(\left[\matrix{X_a\\Y_a}\right] + \left[\matrix{X_b\\Y_b}\right]\) and \(\left[\matrix{X_a\\Y_a\\Z_a}\right] + \left[\matrix{X_b\\Y_b\\Z_b}\right]\)
The following vectors can not be added because they have different numbers of elements.
\(\left[\matrix{X_a\\Y_a}\right] + \left[\matrix{X_b\\Y_b\\Z_b}\right]\)
The following vectors can not be added because they have a different orientation.
\([X_a\;Y_a\;Z_a]+ \left[\matrix{X_b\\Y_b\\Z_b}\right]\)
Example
\(\left[\matrix{a\\b}\right] + \left[\matrix{c\\d}\right] = \left[\matrix{a+c\\b+d}\right]\)
\(\left[\matrix{1\\2}\right] + \left[\matrix{3\\4}\right] = \left[\matrix{1+3\\2+4}\right]=\left[\matrix{4\\6}\right] \)
The addition to higher-dimension vectors is performed according to the same principle.
\(\left[\matrix{a\\b\\c}\right] + \left[\matrix{x\\y\\z}\right] = \left[\matrix{a+x\\b+y\\c+z}\right]\)
\(\left[\matrix{1\\2\\3}\right] + \left[\matrix{10\\20\\30}\right] = \left[\matrix{1+10\\2+20\\3+30}\right] =\left[\matrix{11\\22\\33}\right] \)
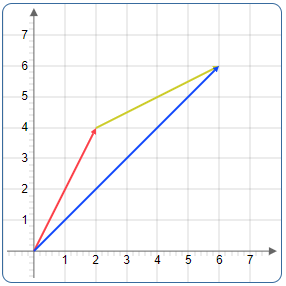
Graphic Vector Additionn
The following figure shows the graphical vector addition of the expression
\(\left[\matrix{2\\4}\right] + \left[\matrix{4\\2}\right] = \left[\matrix{2+4\\4+2}\right]=\left[\matrix{6\\6}\right] \)
First the line of the first vector (red) is drawn from the zero point to the position \(x = 2, y = 4\)
Then, from the top of the first vector, the second vector (yellow) is drawn to the position by 4 units to the right and two units to the top.
The sum vector (blue) is determined by the line from the base point of the first to the peak of the second vector
The subtraction of vectors is identical to the addition of vectors, but with negative operator. For the vector subtraction, the same rules apply as for the addition of the vector.
More information about vector subtraction you can find here.
Vector addition online calculator →
|
|