Vektoraddition
Formeln, Regeln und Beispiele zur Addition von Vektoren
Die Vektoraddition ist eine grundlegende Operation in der Vektorrechnung, bei der zwei oder mehr Vektoren komponentenweise addiert werden. Dies ist eine elementare Operation in der linearen Algebra und hat vielfältige Anwendungen in Physik, Ingenieurwesen und Computergrafik.
Vektoren können nur addiert werden, wenn sie die gleiche Dimension haben und in der gleichen Ausrichtung vorliegen (beide Spalten- oder beide Zeilenvektoren). Die Addition erfolgt durch komponentenweise Addition der entsprechenden Elemente.
Bedingungen für Vektoraddition
- Sie die gleiche Anzahl von Elementen (Komponenten) haben
- Sie in der gleichen Ausrichtung vorliegen (beide Spaltenvektoren oder beide Zeilenvektoren)
- Sie beide aus dem gleichen Vektorraum stammen
✅ Gültige Vektoradditionen
Die folgenden Vektorpaare können addiert werden:
2D-Vektoren (zwei Komponenten)
3D-Vektoren (drei Komponenten)
❌ Ungültige Vektoradditionen
Unterschiedliche Dimension: Vektoren mit 2 und 3 Komponenten können nicht addiert werden
Unterschiedliche Ausrichtung: Reihenvektor + Spaltenvektor kann nicht addiert werden
Formeln der Vektoraddition
Addition von 2D-Vektoren
Allgemeine Form:
Konkretes Beispiel:
Addition von 3D-Vektoren
Allgemeine Form:
Konkretes Beispiel:
Addition von n-dimensionalen Vektoren
Für Vektoren beliebiger Dimension \(n\):
Praktische Beispiele
Beispiel 1: Addition zweier 2D-Vektoren
Gegeben: \(\vec{a} = \begin{bmatrix} 5 \\ 3 \end{bmatrix}\) und \(\vec{b} = \begin{bmatrix} 2 \\ 7 \end{bmatrix}\)
Beispiel 2: Addition zweier 3D-Vektoren
Gegeben: \(\vec{u} = \begin{bmatrix} 1 \\ -2 \\ 4 \end{bmatrix}\) und \(\vec{v} = \begin{bmatrix} 3 \\ 1 \\ -1 \end{bmatrix}\)
Beispiel 3: Addition von drei Vektoren
Gegeben: \(\vec{a} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}\), \(\vec{b} = \begin{bmatrix} 3 \\ 1 \end{bmatrix}\), \(\vec{c} = \begin{bmatrix} 2 \\ 4 \end{bmatrix}\)
Grafische Vektoraddition
Die Vektoraddition kann auch geometrisch interpretiert werden. Dabei wird der erste Vektor vom Ursprung aus gezeichnet, und der zweite Vektor wird mit seinem Startpunkt an die Spitze des ersten Vektors platziert. Der Summenvektor verläuft dann vom Ursprung zur Spitze des zweiten Vektors.
Beispiel: \(\begin{bmatrix} 2 \\ 4 \end{bmatrix} + \begin{bmatrix} 4 \\ 2 \end{bmatrix} = \begin{bmatrix} 6 \\ 6 \end{bmatrix}\)
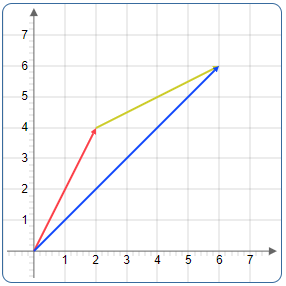
Grafische Darstellung der Vektoraddition: Der erste Vektor (rot) wird vom Ursprung gezeichnet, der zweite Vektor (gelb) an dessen Spitze angehängt, und der Summenvektor (blau) verbindet den Ursprung mit der finalen Spitze
Die Vektoraddition folgt der Parallelogramm-Regel: Wenn zwei Vektoren zwei Seiten eines Parallelogramms bilden, ist die Summenvektor die Diagonale des Parallelogramms.
Eigenschaften der Vektoraddition
- Kommutativität: \(\vec{a} + \vec{b} = \vec{b} + \vec{a}\)
- Assoziativität: \((\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})\)
- Neutrales Element: \(\vec{a} + \vec{0} = \vec{a}\) (Nullvektor)
- Inverses Element: \(\vec{a} + (-\vec{a}) = \vec{0}\)
- Distributivität: \(k(\vec{a} + \vec{b}) = k\vec{a} + k\vec{b}\)
Vektorsubtraktion
Die Vektorsubtraktion ist eng mit der Addition verknüpft. Sie wird durchgeführt, indem die Komponenten des zweiten Vektors von denen des ersten subtrahiert werden.
Allgemeine Formel
Die Vektorsubtraktion folgt den gleichen Regeln wie die Addition und kann auch geometrisch durch die Addition mit dem negativen Vektor interpretiert werden.
Weitere Informationen zur Vektorsubtraktion finden Sie hier.
Zusammenfassung
Definition
Komponentenweise Addition von Vektoren gleicher Dimension
Bedingung
Gleiche Anzahl Komponenten und gleiche Ausrichtung erforderlich
Formel 2D
\[\displaystyle \begin{bmatrix} a_1 \\ a_2 \end{bmatrix} + \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} = \begin{bmatrix} a_1+b_1 \\ a_2+b_2 \end{bmatrix}\]
Formel 3D
\[\displaystyle \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} + \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} = \begin{bmatrix} a_1+b_1 \\ a_2+b_2 \\ a_3+b_3 \end{bmatrix}\]
|
|