Vector Definition
Description of various vectors in the coordinate system
Vectors describe a direction and magnitude in a coordinate system. For calculations we use them as lists of numbers. But for understanding it can help to display them as geometric objects.
The vector \(\underline{x}=\left[\matrix{a\\b}\right]\) has a magniutude \(|\underline{x}|=\sqrt{a^2+b^2}\)
A vector is uniquely determined by length, direction and orientation.
Plot vectors
To draw a vector, use a coordinate system. Draw a horizontal line and a line perpendicular. The horizontal line is the X-axis; the vertical line is the Y-axis. The axes labeled with numbers for the scales of the corresponding units.
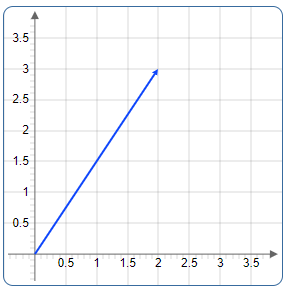
The following figure shows the vector \(\overrightarrow{a}=\left[\matrix{x\\y}\right]\) or \(\overrightarrow{a}=\left[\matrix{2\\3}\right]\)
The top number is the x coordinate and the bottom is the y coordinate of the vector.
To draw the vector (2, 3), drag from a starting point a line 2 units to the right on the x-axis and 3 units up on the y-axis
The vector is uniquely defined by its direction and its length.
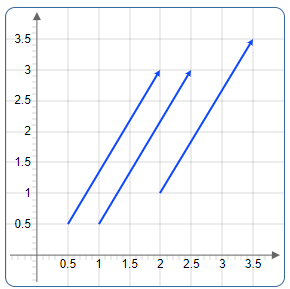
Equal Vectors
The following figure shows parallel vectors of equal length, direction and orientation. Since the location of a vector is arbitrary, these vectors are equal.
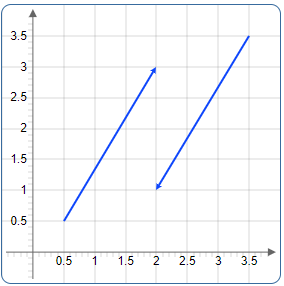
Opposite Vectors
Parallel vectors of equal length but opposite in orientation are called opposite vector.
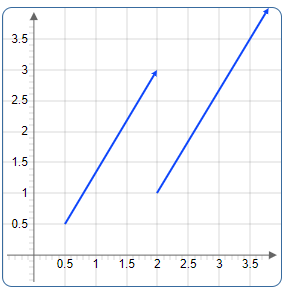
Parallel Vectors
Two vectors are called in parallel if they have the same direction. They can be different lengths and have opposite orientations.
|
|