Vector Magnitude
Formulas and examples to calculate the magnitude of a vector
This article describes how to calculate the magnitude of a vector. The magnitude of a vector is the length of the vector and can be calculated using the Pythagoras theorem. According to this, the square of the hypotenuse is equal to the sum of the squares of the catheters. The lengths of the catheters correspond to the respective coordinates of the vector.
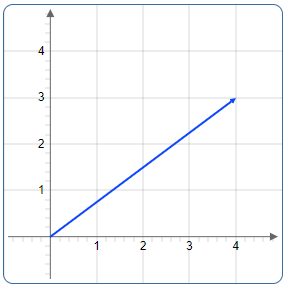
The following illustration shows the vector \(\left[\matrix{4\\3}\right]\) in a plane.
The length of the vector corresponds to the length of the hypotenuse of a right triangle.
We can therefore calculate for the vector \(\displaystyle \left[\matrix{a\\b}\right]\) \(\displaystyle |v|=\sqrt{a^2+b^2}\)
Example
\(|v|=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5\)
The same procedure applies to vectors with more than two elements.
\(\left|\left[\matrix{1\\2\\2}\right]\right|=\sqrt{1^2+2^2+2^2}=\sqrt{1+4+4}=\sqrt{9}=3\)
\(\left|\left[\matrix{-4\\6\\-12}\right]\right|=\sqrt{(-4)^2+6^2+(-12)^2}=\sqrt{16+36+144}=\sqrt{196}=14\)
Magnitude online calculator →
|
|