Vektoren Definition

Grundlagen und Definitionen von Vektoren im Koordinatensystem

Ein Vektor ist in der Mathematik ein Objekt, das durch zwei Charakteristika definiert wird: Größe (Betrag) und Richtung. Vektoren werden im Koordinatensystem als Zahlenlisten dargestellt, können aber auch geometrisch als Pfeile visualisiert werden, die vom Ursprung zu einem bestimmten Punkt zeigen.

Vektoren sind fundamental in Mathematik, Physik und Ingenieurwesen, da sie es ermöglichen, physikalische Größen wie Kraft, Geschwindigkeit oder Verschiebung kompakt und präzise zu beschreiben.

Grundelemente eines Vektors

Magnitude (Betrag)

Länge oder Größe des Vektors

Richtung

Richtung im Koordinatensystem

Komponenten

Einzelne Zahlenwerte (x, y, z, ...)

Orientierung

Richtungssinn (von-nach)

Ein Vektor ist eindeutig bestimmt durch:
  • Seine Länge (Magnitude oder Betrag)
  • Seine Richtung im Raum
  • Seine Orientierung (Anfangs- und Endpunkt)
  • Die Position ist nicht eindeutig - Vektoren können verschoben werden

Notation und Darstellung

Schreibweisen für Vektoren

Vektoren können auf verschiedene Arten notiert werden:

\[\displaystyle \vec{a} = \overrightarrow{a} = \mathbf{a} = \begin{bmatrix} a_1 \\ a_2 \end{bmatrix} \text{ (2D-Vektor)}\]

Für einen 2D-Vektor mit Komponenten \(x\) und \(y\):

\[\displaystyle \vec{v} = \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} v_x \\ v_y \end{bmatrix}\]

Für einen 3D-Vektor mit Komponenten \(x\), \(y\) und \(z\):

\[\displaystyle \vec{v} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} v_x \\ v_y \\ v_z \end{bmatrix}\]

Beispiel: Der Vektor \(\vec{a} = \begin{bmatrix} 2 \\ 3 \end{bmatrix}\) hat die x-Komponente 2 und die y-Komponente 3.

Betrag eines Vektors

Der Betrag oder die Magnitude eines Vektors ist seine Länge. Sie wird berechnet, indem die geometrische Interpretation des Vektors als Hypotennuse eines rechtwinkligen Dreiecks verwendet wird.

Betrag in 2D

\[\displaystyle |\vec{v}| = \left|\begin{bmatrix} x \\ y \end{bmatrix}\right| = \sqrt{x^2 + y^2}\]

Betrag in 3D

\[\displaystyle |\vec{v}| = \left|\begin{bmatrix} x \\ y \\ z \end{bmatrix}\right| = \sqrt{x^2 + y^2 + z^2}\]

Allgemeine Form

\[\displaystyle |\vec{v}| = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2}\]

Beispiel: Der Betrag des Vektors \(\vec{a} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}\) ist:

\[\displaystyle |\vec{a}| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\]

Vektoren im Koordinatensystem

Um Vektoren zu visualisieren, verwendet man ein Koordinatensystem mit zwei oder mehr Achsen. Im 2D-Fall sind dies die X-Achse (horizontal) und die Y-Achse (vertikal).

Um einen Vektor \(\vec{v} = \begin{bmatrix} 2 \\ 3 \end{bmatrix}\) zu zeichnen:

  • Starten Sie am Ursprung (0, 0)
  • Gehen Sie 2 Einheiten in x-Richtung nach rechts
  • Gehen Sie 3 Einheiten in y-Richtung nach oben
  • Zeichnen Sie einen Pfeil vom Ursprung zum Endpunkt (2, 3)
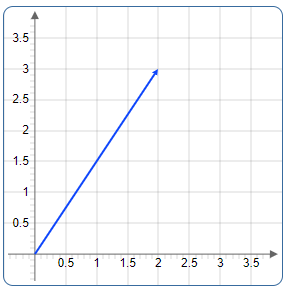
Vektor im Koordinatensystem

Vektor \(\vec{a} = \begin{bmatrix} 2 \\ 3 \end{bmatrix}\) im Koordinatensystem mit Magnitude \(|\vec{a}| = \sqrt{13} \approx 3.61\)

Gleiche Vektoren

Zwei Vektoren sind gleich, wenn sie die gleiche Länge, Richtung und Orientierung haben. Die Position im Koordinatensystem ist irrelevant - nur die Komponenten zählen.

Definition von Gleichheit

\[\displaystyle \vec{a} = \vec{b} \iff \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix} \iff a_i = b_i \text{ für alle } i\]

Geometrisch bedeutet das: Gleiche Vektoren sind parallel verschobene Kopien voneinander. Sie liegen nicht notwendigerweise am gleichen Ort, sondern haben nur die gleichen Eigenschaften.

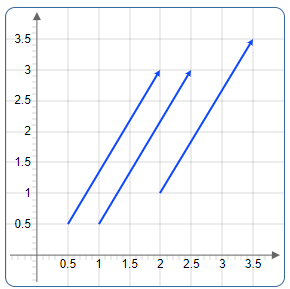
Gleiche Vektoren

Gleiche Vektoren: Alle drei Pfeile haben die gleiche Länge und Richtung, daher sind sie gleich

Gegenvektor

Der Gegenvektor (oder negative Vektor) eines Vektors \(\vec{a}\) ist ein Vektor, der die gleiche Länge, aber die entgegengesetzte Richtung und Orientierung hat.

Definition des Gegenvektors

\[\displaystyle -\vec{a} = -\begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix} = \begin{bmatrix} -a_1 \\ -a_2 \\ \vdots \\ -a_n \end{bmatrix}\]

Beispiel:

\[\displaystyle \vec{a} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} \implies -\vec{a} = \begin{bmatrix} -2 \\ -3 \end{bmatrix}\]

Wichtige Eigenschaft: \(\vec{a} + (-\vec{a}) = \vec{0}\) (Nullvektor)

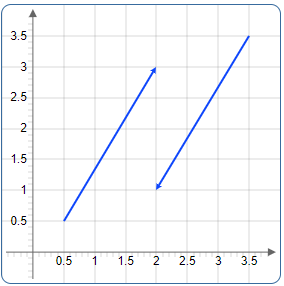
Gegenvektor

Gegenvektor: Der blaue Vektor ist der Gegenvektor des roten Vektors - gleiche Länge, entgegengesetzte Richtung

Parallele Vektoren

Zwei Vektoren sind parallel, wenn sie in die gleiche oder entgegengesetzte Richtung zeigen. Sie können unterschiedliche Längen haben, müssen aber kollinear sein (auf einer Geraden liegen).

Definition von Parallelität

Vektoren \(\vec{a}\) und \(\vec{b}\) sind parallel, wenn es ein Skalar \(\lambda\) gibt, so dass:

\[\displaystyle \vec{b} = \lambda \vec{a} \quad \text{mit} \quad \lambda \in \mathbb{R}, \lambda \neq 0\]

Beispiele:

  • \(\vec{a} = \begin{bmatrix} 2 \\ 3 \end{bmatrix}\) und \(\vec{b} = \begin{bmatrix} 4 \\ 6 \end{bmatrix}\) sind parallel, da \(\vec{b} = 2\vec{a}\)
  • \(\vec{a} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}\) und \(\vec{c} = \begin{bmatrix} -2 \\ -4 \end{bmatrix}\) sind parallel, da \(\vec{c} = -2\vec{a}\)
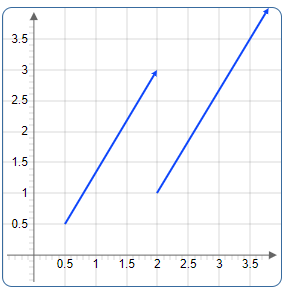
Parallele Vektoren

Parallele Vektoren: Alle Vektoren zeigen in die gleiche Richtung oder entgegengesetzt, können aber unterschiedliche Längen haben

Spezielle Vektoren

Wichtige Vektortypen:
  • Nullvektor \(\vec{0}\): Vektor mit Betrag 0, alle Komponenten sind 0
  • Einheitsvektor: Vektor mit Betrag 1 (wird mit \(\hat{u}\) oder \(\vec{e}\) notiert)
  • Basisvektoren: \(\vec{e}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\) und \(\vec{e}_2 = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\) im 2D-Fall
  • Ortsvektor: Vektor vom Ursprung zu einem Punkt

Normalisierung eines Vektors (zu Einheitsvektor)

\[\displaystyle \hat{v} = \frac{\vec{v}}{|\vec{v}|} = \frac{1}{\sqrt{v_1^2 + v_2^2 + \cdots + v_n^2}} \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}\]

Zusammenfassung

Definition

Objekt mit Größe und Richtung, dargestellt als Zahlenliste oder Pfeil

Betrag

\[\displaystyle |\vec{v}| = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2}\]

Gleichheit

Zwei Vektoren sind gleich, wenn alle Komponenten gleich sind

Parallelität

\[\displaystyle \vec{b} = \lambda \vec{a} \text{ für ein Skalar } \lambda\]



Weitere Vektor Berechnungen

Vektor Definition
Vektor berechnen
Vektor Addition
Vektor Subtraktion
Vektor Betrag
Vektor Skalarprodukt
Vektor Kreuzprodukt
Winkel zwischen Vektoren
Vektor Spatprodukt
















Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?