Winkel zwischen zwei Vektoren berechnen
Online Rechner zur Berechnung des Winkels zwischen zwei Vektoren im 2D und 3D Raum
Vektor-Winkel Rechner
Winkel zwischen Vektoren
Berechnet den Winkel θ zwischen zwei Vektoren a⃗ und b⃗ mittels Skalarprodukt im 2D oder 3D Raum.
Visualisierung
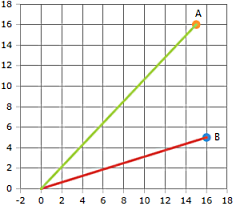
Die Grafik zeigt zwei Vektoren mit ihrem gemeinsamen Ursprung und dem eingeschlossenen Winkel.
Der Winkel wird über das Skalarprodukt und die Vektorlängen berechnet.
|
|
Was ist der Winkel zwischen zwei Vektoren?
Der Winkel zwischen zwei Vektoren ist der kleinste Winkel zwischen ihren Richtungen:
- Bereich: 0° bis 180° (0 bis π Radiant)
- Gemeinsamer Ursprung: Vektoren starten vom selben Punkt
- Richtungsabhängig: Nur die Richtung, nicht die Position zählt
- 0°: Vektoren zeigen in dieselbe Richtung
- 90°: Vektoren stehen senkrecht zueinander
- 180°: Vektoren zeigen in entgegengesetzte Richtungen
Berechnung über das Skalarprodukt
Die Winkelberechnung erfolgt über das Skalarprodukt der Vektoren:
Skalarprodukt
Summe der Komponentenprodukte
Vektorlängen
Euklidische Norm der Vektoren
2D und 3D Vektoren
Der Rechner unterstützt sowohl 2D- als auch 3D-Vektoren:
2D Vektoren
Vektoren in der Ebene (x, y)
3D Vektoren
Vektoren im Raum (x, y, z)
Formeln zur Winkelberechnung
Hauptformel - Winkel über Skalarprodukt
Kosinus des Winkels durch normiertes Skalarprodukt
Skalarprodukt 2D
Skalarprodukt in der Ebene
Skalarprodukt 3D
Skalarprodukt im Raum
Vektorlänge 2D
Länge in der Ebene
Vektorlänge 3D
Länge im Raum
Winkel berechnen
Arkuskosinus des normierten Skalarprodukts
Beispiel
Beispielrechnung (2D)
1. Skalarprodukt
Summe der Komponentenprodukte
2. Vektorlängen
Längen der beiden Vektoren
3. Kosinus berechnen
Normiertes Skalarprodukt
4. Winkel
Der Winkel beträgt etwa 38.7°
Vektorwinkel in der linearen Algebra
Der Winkel zwischen zwei Vektoren ist ein fundamentales Konzept der linearen Algebra und Geometrie. Er beschreibt die Richtungsbeziehung zwischen zwei Vektoren unabhängig von ihrer Position im Raum und wird ausschließlich über das Skalarprodukt und die Vektorlängen berechnet.
Mathematische Grundlagen
Die Winkelberechnung basiert auf der geometrischen Interpretation des Skalarprodukts:
Durch Umstellung nach dem Kosinus erhalten wir die Winkelformel:
Berechnung Schritt für Schritt
- Skalarprodukt berechnen: Summe der Komponentenprodukte
- Vektorlängen bestimmen: Euklidische Norm jedes Vektors
- Kosinus berechnen: Skalarprodukt geteilt durch Längenprodukt
- Winkel ermitteln: Arkuskosinus des berechneten Wertes
Besondere Winkelwerte
0° (Parallelität)
cos(θ) = 1
Vektoren zeigen in gleiche Richtung
90° (Orthogonalität)
cos(θ) = 0
Vektoren stehen senkrecht
180° (Antiparallelität)
cos(θ) = -1
Vektoren zeigen in entgegengesetzte Richtungen
Anwendungen in der Praxis
Die Winkelberechnung zwischen Vektoren findet sich in vielen Bereichen:
- Computergrafik: Beleuchtungsberechnungen, Normalenvektoren
- Physik: Kraft- und Geschwindigkeitsvektoren, Drehmomente
- Maschinelles Lernen: Ähnlichkeitsmessungen, Datenanalyse
- Robotik: Bewegungsplanung, Orientierungsbestimmung
- Navigation: Richtungsbestimmung, GPS-Berechnungen
- Kristallografie: Bindungswinkel in Molekülen
Eigenschaften des Vektorwinkels
Kommutativität
Der Winkel zwischen a⃗ und b⃗ ist gleich dem zwischen b⃗ und a⃗.
Dimensionsunabhängigkeit
Die Formel funktioniert gleichermaßen für 2D, 3D und höhere Dimensionen.
Skalierungsinvarianz
Die Länge der Vektoren beeinflusst den Winkel nicht, nur die Richtung zählt.
Wertebereich
Der Winkel liegt immer zwischen 0° und 180° (0 und π Radiant).
Verwandte Konzepte
Das Skalarprodukt und der Vektorwinkel sind eng mit anderen mathematischen Konzepten verbunden:
- Orthogonalität: Zwei Vektoren sind orthogonal, wenn ihr Skalarprodukt null ist
- Projektion: Die Projektion eines Vektors auf einen anderen hängt vom Winkel ab
- Kosinussatz: Der Vektorwinkel verallgemeinert den Kosinussatz für n-dimensionale Räume
- Norm und Metrik: Der Winkel definiert eine natürliche Metrik im Vektorraum
|
|
|
|