Calculate Angle Between Two Vectors
Online calculator for calculating the angle between two vectors in 2D and 3D space
Vector Angle Calculator
Angle Between Vectors
Calculates the angle θ between two vectors a⃗ and b⃗ using the dot product in 2D or 3D space.
Visualization
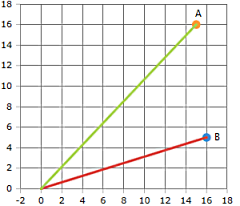
The graphic shows two vectors with their common origin and the included angle.
The angle is calculated using the dot product and vector lengths.
|
|
What is the Angle Between Two Vectors?
The angle between two vectors is the smallest angle between their directions:
- Range: 0° to 180° (0 to π radians)
- Common origin: Vectors start from the same point
- Direction dependent: Only direction matters, not position
- 0°: Vectors point in the same direction
- 90°: Vectors are perpendicular to each other
- 180°: Vectors point in opposite directions
Calculation via Dot Product
The angle calculation is done using the dot product of the vectors:
Dot Product
Sum of component products
Vector Lengths
Euclidean norm of the vectors
2D and 3D Vectors
The calculator supports both 2D and 3D vectors:
2D Vectors
Vectors in the plane (x, y)
3D Vectors
Vectors in space (x, y, z)
Formulas for Angle Calculation
Main Formula - Angle via Dot Product
Cosine of the angle through normalized dot product
Dot Product 2D
Dot product in the plane
Dot Product 3D
Dot product in space
Vector Length 2D
Length in the plane
Vector Length 3D
Length in space
Calculate Angle
Arccosine of the normalized dot product
Example
Example Calculation (2D)
1. Dot Product
Sum of component products
2. Vector Lengths
Lengths of both vectors
3. Calculate Cosine
Normalized dot product
4. Angle
The angle is approximately 38.7°
Vector Angles in Linear Algebra
The angle between two vectors is a fundamental concept in linear algebra and geometry. It describes the directional relationship between two vectors regardless of their position in space and is calculated exclusively using the dot product and vector lengths.
Mathematical Foundations
The angle calculation is based on the geometric interpretation of the dot product:
By rearranging for the cosine, we get the angle formula:
Step-by-Step Calculation
- Calculate dot product: Sum of component products
- Determine vector lengths: Euclidean norm of each vector
- Calculate cosine: Dot product divided by length product
- Find angle: Arccosine of the calculated value
Special Angle Values
0° (Parallel)
cos(θ) = 1
Vectors point in same direction
90° (Orthogonal)
cos(θ) = 0
Vectors are perpendicular
180° (Anti-parallel)
cos(θ) = -1
Vectors point in opposite directions
Practical Applications
Vector angle calculation is found in many areas:
- Computer graphics: Lighting calculations, normal vectors
- Physics: Force and velocity vectors, torques
- Machine learning: Similarity measurements, data analysis
- Robotics: Motion planning, orientation determination
- Navigation: Direction finding, GPS calculations
- Crystallography: Bond angles in molecules
Properties of Vector Angles
Commutativity
The angle between a⃗ and b⃗ equals the angle between b⃗ and a⃗.
Dimension Independence
The formula works equally for 2D, 3D and higher dimensions.
Scale Invariance
Vector length doesn't affect the angle, only direction matters.
Value Range
The angle always lies between 0° and 180° (0 and π radians).
Related Concepts
The dot product and vector angle are closely related to other mathematical concepts:
- Orthogonality: Two vectors are orthogonal when their dot product is zero
- Projection: The projection of one vector onto another depends on the angle
- Law of cosines: The vector angle generalizes the law of cosines for n-dimensional spaces
- Norm and metric: The angle defines a natural metric in vector space
|
|
|
|