Steigung einer Geraden berechnen
Online Rechner zum Berechnen der Steigung zwischen zwei Punkten
Steigung Rechner
Steigung einer Geraden
Die Steigung m einer Geraden beschreibt, um wie viele Einheiten sich der Y-Wert ändert, wenn der X-Wert um eine Einheit zunimmt.
Visualisierung
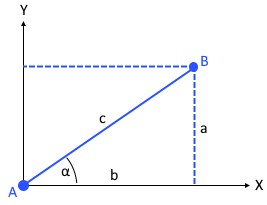
Die Grafik zeigt die Steigung als Verhältnis von Höhenunterschied zu horizontaler Entfernung.
Das Steigungsdreieck verdeutlicht die geometrische Bedeutung der Steigung.
|
|
Was ist die Steigung einer Geraden?
Die Steigung gibt an, wie stark eine Gerade ansteigt oder abfällt:
- Positive Steigung: Gerade steigt von links nach rechts
- Negative Steigung: Gerade fällt von links nach rechts
- Steigung = 0: Horizontale Gerade (parallel zur X-Achse)
- Steigung = 1: 45° Anstieg (m = tan(45°))
- Große Steigung: Steile Gerade
- Kleine Steigung: Flache Gerade
Zusammenhang zwischen Steigung und Winkel
Die Steigung und der Neigungswinkel stehen in direkter Beziehung zueinander:
Steigung aus Winkel
Steigung ist der Tangens des Winkels
Winkel aus Steigung
Winkel ist der Arkustangens der Steigung
Formeln zur Steigungsberechnung
Hauptformel - Steigung zwischen zwei Punkten
Steigung = Änderung in Y-Richtung ÷ Änderung in X-Richtung
Winkel zur X-Achse (Arkussinus)
Berechnung über den Sinus des Steigungsdreiecks
Winkel zur X-Achse (Arkuskosinus)
Berechnung über den Kosinus des Steigungsdreiecks
Entfernung zwischen Punkten
Hypotenuse des Steigungsdreiecks
Steigung über Tangens
Direkter Zusammenhang zwischen Steigung und Winkel
Beispiel
Beispielrechnung
Steigung berechnen
Die Steigung beträgt 4/3 ≈ 1,33
Winkel berechnen
Der Neigungswinkel beträgt etwa 53,13°
Interpretation
- Steigung 4/3: Pro 3 X-Einheiten steigt Y um 4
- Positive Steigung: Gerade steigt an
- Steiler Anstieg: Winkel > 45°
Anwendungen
Straßenneigung, Dachneigung, Geländeprofile, technische Zeichnungen.
Steigung in der Praxis verstehen
Die Steigung einer Geraden ist ein fundamentales Konzept in der Mathematik und beschreibt, wie stark eine Linie ansteigt oder abfällt. Sie ist definiert als das Verhältnis der vertikalen Änderung zur horizontalen Änderung zwischen zwei Punkten.
Geometrische Bedeutung
Die Steigung m einer Geraden zwischen zwei Punkten A(x₁,y₁) und B(x₂,y₂) wird berechnet als:
Arten der Steigung
Positive Steigung (m > 0)
Die Gerade steigt von links nach rechts an. Je größer der Wert, desto steiler der Anstieg.
Negative Steigung (m < 0)
Die Gerade fällt von links nach rechts ab. Je negativer der Wert, desto steiler der Abfall.
Nullsteigung (m = 0)
Die Gerade verläuft horizontal. Es gibt keine Änderung in Y-Richtung.
Unendliche Steigung
Bei vertikalen Geraden ist die Steigung nicht definiert (Division durch Null).
Praktische Anwendungen
Die Steigungsberechnung findet sich in vielen praktischen Bereichen:
- Bauwesen: Dachneigungen, Rampen, Straßensteigungen
- Geografie: Geländeprofile, Höhenlinien in Karten
- Wirtschaft: Wachstumsraten, Trends in Diagrammen
- Physik: Geschwindigkeits-Zeit-Diagramme, Kraft-Weg-Diagramme
- Technik: Maschinenbau, Elektronik (Kennlinien)
Besondere Steigungswerte
m = 1
45° Anstieg
α = arctan(1) = 45°
m = √3 ≈ 1,73
60° Anstieg
α = arctan(√3) = 60°
m = 1/√3 ≈ 0,58
30° Anstieg
α = arctan(1/√3) = 30°
|
|
|
|