Calculate Belt Length

Calculator and formulas for calculating the belt length of a drive

Belt Length Calculator

Calculate belt drive

Calculates the belt length of a drive with two pulleys or the center distance when the belt length is given.

Pulleys
Belt drive with two pulleys
mm
mm
mm
Result
Belt length:

Applications

Practical Applications
Mechanical engineering: V-belts, flat belts, timing belts
Automotive engineering: Engine belts, auxiliary drive belts
Conveyor technology: Conveyor belts, transport belts
Belt Types
  • V-belt: V-shaped cross-section
  • Flat belt: Rectangular cross-section
  • Timing belt: With teeth
  • Round belt: Circular cross-section
  • Poly belt: Multi-V belt
  • Timing belt: Synchronous belt

Formulas for belt length

The belt length is calculated from the geometry of the two pulleys and their distance. The exact formula considers both the straight sections and the wrap angles.

Exact belt length formula

Precise calculation for any pulley diameters and center distances.

\[L = (d_1 + d_2) \cdot \frac{\pi}{2} + (d_1 - d_2) \cdot \arcsin\left(\frac{d_1 - d_2}{2 \cdot D}\right) + 2 \cdot \sqrt{D^2 - 0.25 \cdot (d_1 - d_2)^2}\]
This formula is used by the calculator and is accurate for all configurations.
Approximate formula

Simplified calculation for similar pulley diameters.

\[L ≈ \frac{\pi}{2} \cdot (d_1 + d_2) + 2 \cdot D + \frac{(d_1 - d_2)^2}{4 \cdot D}\]
Good for similar pulleys or large center distances.
Calculate center distance

Inverse calculation for center distance with given belt length.

\[D = \frac{b + \sqrt{b^2 - 32 \cdot (d_1 - d_2)^2}}{16}\] \[b = 4 \cdot L - 2 \cdot \pi \cdot (d_1 + d_2)\]
For design with predetermined belt.
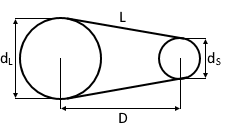
Symbols and Units
  • L = Belt length
  • d₁ = Diameter of large pulley
  • d₂ = Diameter of small pulley
  • D = Center distance (center to center)
  • Units: All measurements in same unit
  • Note: Use diameters, not radii
Example: V-belt drive
Problem:

A V-belt drive has a driving pulley with 150 mm diameter and a driven pulley with 300 mm diameter. The center distance is 600 mm. What belt length is required?

Given:
  • Diameter Pulley 1: d₁ = 150 mm
  • Diameter Pulley 2: d₂ = 300 mm
  • Center distance: D = 600 mm
  • Find: Belt length L
Solution:
\[L = (d_1 + d_2) \cdot \frac{\pi}{2} + (d_1 - d_2) \cdot \arcsin\left(\frac{d_1 - d_2}{2 \cdot D}\right)\] \[+ 2 \cdot \sqrt{D^2 - 0.25 \cdot (d_1 - d_2)^2}\]
\[L = (150 + 300) \cdot \frac{\pi}{2} + (150 - 300) \cdot \arcsin\left(\frac{150 - 300}{2 \cdot 600}\right)\] \[+ 2 \cdot \sqrt{600^2 - 0.25 \cdot (150 - 300)^2}\]
\[L ≈ 707.1 + (-150) \cdot (-0.1253) + 2 \cdot 594.4\] \[L ≈ 707.1 + 18.8 + 1188.8 = 1914.7 \text{ mm}\]

Detailed description of belt length calculation

Physical Fundamentals

This function calculates the belt length of a drive with two pulleys or the center distance when the belt length is given.

Usage Instructions

To calculate, select with the radio buttons whether the belt length or center distance should be calculated. Then enter the required values and click the 'Calculate' button. Diameters, distances and length have the same unit (e.g. meters or cm).

Application Areas

Mechanical Engineering

V-belts, flat belts, timing belts, industrial drives. Dimensioning of belt drives and transmission systems.

Automotive Engineering

Engine belts, auxiliary drive belts, alternator, water pump. Calculation of belt lengths for vehicle engines.

Conveyor Technology

Conveyor belts, transport belts, belt drives. Design of conveyor systems and transport systems.

Understanding Belt Drives

A belt drive transmits torque through friction between belt and pulleys. The geometry determines the required belt length:

Straight Sections

Run 1: Upper straight part
Run 2: Lower straight part
Length: 2 × tangent length
Calculation: Geometric

Wrap Angles

Large pulley: Partial arc
Small pulley: Larger arc
Sum: < Full circle
Calculation: Trigonometric

Total Length

L = Straight parts + Arcs
Exact: Arcsin formula
Approximate: For similar diameters
Application: Depends on accuracy

Important: The exact formula works well for all pulley ratios. The approximate formula fails for large diameter differences and small center distances.


More physics functions

Centrifugal Force • Efficiency • Inclined plan • kW - hp converter • PS - hp converter • Power Force Displacement and Time • Pressure, Force and Area • Torque • Weight Force • Work, Force and Displacement • Work Power and Time • Energy Density • Kinetic Energy • Specific Energy • Acceleration by Distance • Acceleration by Time • Angular Velocity • Circular Motion • Rotational Speed • Speed, Distance and Time • Free-Fall • Temperature in Atmosphere • Mach Number • Speed of sound • Sound Pressure • Belt Length • Gear Ratio • Angle of refraction