Calculate Inclined Plane

Calculator and formulas for calculating an inclined plane

Inclined Plane Calculator

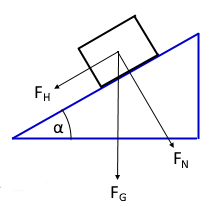
Force decomposition on inclined plane

Calculates the force components on an inclined plane: Weight force (FG), Downhill force (FH) and Normal force (FN).

Inclined Plane
Forces on the inclined plane
N
Result
Weight force FG:
Downhill force FH:
Normal force FN:

Example Calculation

Example: Box on inclined plane
Problem:

A box with 50 kg mass lies on an inclined plane with 30° inclination. Calculate all force components (g = 9.81 m/s²).

Given:
  • Mass m = 50 kg
  • Inclination angle α = 30°
  • g = 9.81 m/s²
  • FG = m × g = 50 × 9.81 = 490.5 N
Solution:
Downhill force (FH):
\[F_H = F_G \times \sin(\alpha)\] \[F_H = 490.5 \text{ N} \times \sin(30°)\] \[F_H = 490.5 \times 0.5 = 245.25 \text{ N}\]
Normal force (FN):
\[F_N = F_G \times \cos(\alpha)\] \[F_N = 490.5 \text{ N} \times \cos(30°)\] \[F_N = 490.5 \times 0.866 = 424.8 \text{ N}\]
Practical Applications
Road construction: Calculation of downhill forces for vehicles
Mechanical engineering: Conveyor belts, slides, ramps
Construction: Roof structures, stairs, slopes
Important Angle Values
  • 0°: sin = 0, cos = 1
  • 30°: sin = 0.5, cos = 0.866
  • 45°: sin = 0.707, cos = 0.707
  • 60°: sin = 0.866, cos = 0.5
  • 90°: sin = 1, cos = 0
  • Gradient 1:3 ≈ 18.4°

Formulas for inclined plane

On an inclined plane the weight force is decomposed into two components: the downhill force (parallel to the plane) and the normal force (perpendicular to the plane).

Downhill force FH

Force component parallel to the inclined plane (sliding force).

\[\displaystyle F_H = F_G \cdot \sin(\alpha)\]
Causes movement along the plane.
Normal force FN

Force component perpendicular to the inclined plane.

\[\displaystyle F_N = F_G \cdot \cos(\alpha)\]
Presses the body against the plane.
Weight force FG

Resultant from both components.

\[\displaystyle F_G = \sqrt{F_H^2 + F_N^2}\]
Or: FG = m × g
Important Notes
  • At α = 0°: FH = 0 and FN = FG (horizontal plane)
  • At α = 90°: FH = FG and FN = 0 (vertical fall)
  • The downhill force increases with increasing inclination angle
  • The normal force decreases with increasing inclination angle

Detailed description of the inclined plane

Physical Fundamentals

This function calculates the forces acting on an inclined plane. The weight force FG can be divided into a component perpendicular to the inclined plane (normal force component FN) and a component parallel to the inclined plane (downhill force FH).

Usage Instructions

Enter a known force (FG, FH or FN) and the inclination angle. The calculator automatically calculates all other force components.

Application Areas

Road and Path Construction

Calculation of downhill forces for vehicles on inclined roads. Important for braking distances and traction.

Mechanical Engineering

Conveyor belts, slides, ramps, inclined conveyor systems. Dimensioning of drives and braking systems.

Construction

Roof structures, stairs, slopes, slip safety. Static calculations for inclined components.

Understanding Force Decomposition

Force decomposition on the inclined plane is a fundamental concept in mechanics. The steeper the plane, the greater the downhill force becomes:

Flat plane (15°)

FH = FG × sin(15°) ≈ 0.26 × FG
FN = FG × cos(15°) ≈ 0.97 × FG

Medium inclination (45°)

FH = FG × sin(45°) ≈ 0.71 × FG
FN = FG × cos(45°) ≈ 0.71 × FG

Steep plane (75°)

FH = FG × sin(75°) ≈ 0.97 × FG
FN = FG × cos(75°) ≈ 0.26 × FG

Insight: The steeper the plane, the greater the downhill force and the smaller the normal force!


More physics functions

Centrifugal Force • Efficiency • Inclined plan • kW - hp converter • PS - hp converter • Power Force Displacement and Time • Pressure, Force and Area • Torque • Weight Force • Work, Force and Displacement • Work Power and Time • Energy Density • Kinetic Energy • Specific Energy • Acceleration by Distance • Acceleration by Time • Angular Velocity • Circular Motion • Rotational Speed • Speed, Distance and Time • Free-Fall • Temperature in Atmosphere • Mach Number • Speed of sound • Sound Pressure • Belt Length • Gear Ratio • Angle of refraction