Vector Magnitude Calculator

Calculator and formulas for computing the length (magnitude) of a vector

Vector Magnitude Calculator

Vector Length by Pythagoras

Calculates the length (magnitude) of a vector through Pythagorean calculation: |v| = √(x² + y² + z²)

Select Vector Dimension
Plane
Space
Four Components
Enter Vector Components
X value of vector
Y value of vector
Z value of vector
W value of vector

Vector Length (Magnitude)
Magnitude |v|:
Calculation: |v| = √(x² + y² + z²)

Magnitude Info

Magnitude Properties

Magnitude: Always positive or zero

|v| ≥ 0 Pythagorean Theorem Length

Geometric: Distance from origin
Formula: Square root of component squares

Examples
|[3, 4]| = √(3² + 4²) = 5
|[1, 2, 2]| = √(1² + 2² + 2²) = 3
|[0, 0, 0]| = 0 (Zero vector)

Formulas for Vector Magnitude

2D Vector Magnitude
\[\left|\left[\matrix{a\\b}\right]\right| = \sqrt{a^2 + b^2}\]

Pythagorean theorem in the plane

3D Vector Magnitude
\[\left|\left[\matrix{a\\b\\c}\right]\right| = \sqrt{a^2 + b^2 + c^2}\]

Extension to space

4D Vector Magnitude
\[\left|\left[\matrix{a\\b\\c\\d}\right]\right| = \sqrt{a^2 + b^2 + c^2 + d^2}\]

Higher-dimensional generalization

General Formula
\[|\vec{v}| = \sqrt{\sum_{i=1}^n v_i^2}\]

n-dimensional Euclidean norm

Calculation Examples for Vector Magnitude

Example 1: 2D Magnitude
v = [3, 4]
\[|v| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\]

Classic 3-4-5 Triangle

Example 2: 3D Magnitude
v = [1, 2, 2]
\[|v| = \sqrt{1^2 + 2^2 + 2^2} = \sqrt{1 + 4 + 4} = \sqrt{9} = 3\]

Spatial Vector

Geometric Interpretation
Distance from Origin
Vector Length
Euclidean Norm

The magnitude gives the geometric length of the vector

Visual Representation (2D)
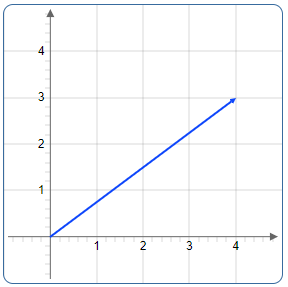
Vector Magnitude Visualization

The magnitude corresponds to the hypotenuse of a right-angled triangle

Applications of Vector Magnitude

Vector magnitude finds application in many scientific and technical fields:

Physics & Mechanics
  • Velocity magnitudes and acceleration
  • Force magnitudes and impulses
  • Magnetic field strengths
  • Wave vectors and frequencies
Computer Graphics
  • Vector normalization
  • Distance calculations
  • Lighting models
  • Collision detection
Navigation & GPS
  • Distance calculations
  • Velocity measurements
  • Route optimization
  • Coordinate distances
Data Analysis
  • Euclidean distances
  • Clustering algorithms
  • Similarity measurements
  • Machine learning metrics

Vector Magnitude: The Euclidean Norm

The vector magnitude or Euclidean norm is the direct generalization of the Pythagorean theorem to arbitrary dimensions. This fundamental operation connects algebraic calculations with geometric distances and forms the foundation for normalizations, distance measurements, and optimization procedures in mathematics and computer science.

Summary

Vector magnitude combines geometric intuition with algebraic precision. The Pythagorean formula - square root of component squares - enables exact length calculations in arbitrary dimensions. From 2D graphics through 3D navigation to high-dimensional data analysis, vector magnitude remains an indispensable tool. It shows how the classical Pythagorean theorem forms the foundation for modern scientific and technical applications.

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?




Vector Functions

Addition • Subtraction • Multiplication • Scalar Multiplication • Division • Scalar Division • Dot Product • Cross Product • Interpolation • Distance • Distance Squaret • Normalization • Reflection • Magnitude • Squared-Magnitude • Triple-Product