Triple Product Calculator

Calculator and formula for calculating the triple product and volume of three vectors

Triple Product Calculator

Triple Product (Scalar Triple Product)

Calculates the triple product (a⃗ × b⃗) · c⃗ of three vectors for volume determination of the spanned parallelepiped

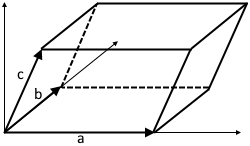
Volume Calculation with Three 3D Vectors

The triple product calculates the volume of the parallelepiped spanned by three vectors in 3D space.

Enter Three 3D Vectors
Vector 1 (a⃗)
Vector 2 (b⃗)
Vector 3 (c⃗)
Triple Product Result
Triple Product (a⃗ × b⃗) · c⃗:
Volume of the spanned parallelepiped
Triple Product = (a⃗ × b⃗) · c⃗ = det(a⃗, b⃗, c⃗) = Volume of parallelepiped

Triple Product Info

Triple Product Properties

Volume: Measures the volume of a 3D parallelepiped

3D Volume Determinant Scalar

Two Methods: (a⃗ × b⃗) · c⃗ or det(a⃗, b⃗, c⃗)
Coplanar: Triple Product = 0 for coplanar vectors

Triple Product Visualization
Parallelepiped spanned by three vectors
Calculation Methods
Method 1: (a⃗ × b⃗) · c⃗
Method 2: det(Matrix)

Formulas for the Triple Product

Cross and Dot Product
\[(\vec{a} \times \vec{b}) \cdot \vec{c}\]

Cross product first, then dot product

Determinant Method
\[\det\begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{pmatrix}\]

Calculate 3×3 determinant

Cross Product Formula
\[\vec{a} \times \vec{b} = \begin{pmatrix} a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{pmatrix}\]

Required for the first method

Volume Interpretation
\[V = |(\vec{a} \times \vec{b}) \cdot \vec{c}|\]

Absolute value for positive volume

Calculation Examples for the Triple Product

Example: Method 1 (Cross & Dot Product)
a⃗=[1,1,1], b⃗=[2,1,3], c⃗=[6,0,-2]
Step 1: Cross Product \[\vec{a} \times \vec{b} = \begin{pmatrix}2\\-1\\-1\end{pmatrix}\] Step 2: Dot Product \[\begin{pmatrix}2\\-1\\-1\end{pmatrix} \cdot \begin{pmatrix}6\\0\\-2\end{pmatrix} = 12+0+2 = 14\]

Triple Product = 14

Example: Method 2 (Determinant)
Same vectors as matrix
\[\det\begin{pmatrix} 1 & 2 & 6 \\ 1 & 1 & 0 \\ 1 & 3 & -2 \end{pmatrix}\] \[= 1 \cdot 1 \cdot (-2) + 2 \cdot 0 \cdot 1 + 6 \cdot 1 \cdot 3\] \[- 6 \cdot 1 \cdot 1 - 1 \cdot 0 \cdot 3 - 2 \cdot 1 \cdot (-2) = 14\]

Triple Product = 14 (same!)

Geometric Meaning
Triple Product > 0
Right-handed system
Triple Product < 0
Left-handed system
Triple Product = 0
Coplanar (in one plane)
|Triple Product|
Volume of parallelepiped

The sign indicates orientation, the magnitude indicates volume

Step-by-Step Instructions
Method 1: Cross & Dot Product
  1. Calculate cross product a⃗ × b⃗
  2. Calculate dot product (a⃗ × b⃗) · c⃗
  3. Result is the triple product
Method 2: Determinant
  1. Form matrix from three vectors
  2. Calculate 3×3 determinant
  3. Determinant is the triple product

Applications of the Triple Product

The triple product is fundamental for 3D geometry and has important applications:

Geometry & 3D Modeling
  • Volume calculation of parallelepipeds
  • Orientation test (right/left-handed system)
  • Check coplanarity of three vectors
  • 3D object recognition and classification
Computer Graphics
  • Backface culling and visibility
  • 3D collision detection
  • Normals and tangent planes
  • Ray tracing and lighting calculations
Physics & Engineering
  • Angular momentum and torque calculations
  • Fluid mechanics: vorticity
  • Crystallography: unit cells
  • Electromagnetism: field calculations
Mathematics & Algebra
  • Check linear independence
  • Basis vectors and coordinate systems
  • Determinants of 3×3 matrices
  • Vector space dimensionality

Triple Product: Volume in Three-Dimensional Space

The triple product is a fundamental operation of 3D vector calculus, assigning a real number to three vectors - the volume of the parallelepiped spanned by them. This elegant combination of cross and dot product, or alternatively the calculation as a 3×3 determinant, reveals deep geometric relationships. The triple product determines coplanarity, establishes orientation, and quantifies three-dimensional extent - indispensable in geometry, physics, and computer graphics.

Summary

The triple product unites geometric intuition with algebraic precision. The two equivalent calculation methods - via cross and dot product or as a determinant - offer both conceptual clarity and computational flexibility. From volume determination through orientation tests to linear independence checking, the triple product opens up fundamental properties of three-dimensional space. It demonstrates how elegantly vector calculus can encode complex spatial relationships in a single number and make them measurable.




Vector Functions

Addition • Subtraction • Multiplication • Scalar Multiplication • Division • Scalar Division • Dot Product • Cross Product • Interpolation • Distance • Distance Squaret • Normalization • Reflection • Magnitude • Squared-Magnitude • Triple-Product