Vector Subtraction

Calculator and formula for subtracting vectors (component-wise difference)

Vector Subtraction Calculator

Vector Subtraction

Calculates the difference v₁ - v₂ of two vectors through component-wise subtraction: [x₁-x₂, y₁-y₂, z₁-z₂]

Requirements for Subtraction

Vectors can only be subtracted if they have the same dimension and the same orientation (column or row vectors).

Select Vector Dimension
Minuend (v₁)
Subtrahend (v₂)
Subtraction Result
X:
Y:
Z:
W:
Difference Vector:
Component-wise subtraction: v₁ - v₂ = [x₁-x₂, y₁-y₂, ...]

Subtraction Info

Subtraction Properties

Component-wise: Corresponding elements are subtracted

v₁ - v₂ Difference Component-wise

Not commutative: v₁ - v₂ ≠ v₂ - v₁
Dimension: Same number of components required

Graphic Representation
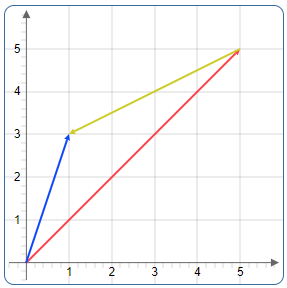
Vector Subtraction
Geometric interpretation of vector subtraction
Examples
[3,5] - [1,4] = [2,1]
[10,20,30] - [1,2,3] = [9,18,27]
[a,b,c] - [x,y,z] = [a-x,b-y,c-z]

Formulas for Vector Subtraction

General Formula
\[\vec{a} - \vec{b} = \begin{pmatrix} a_1 - b_1 \\ a_2 - b_2 \\ \vdots \\ a_n - b_n \end{pmatrix}\]

Component-wise subtraction

2D Subtraction
\[\begin{pmatrix} a \\ b \end{pmatrix} - \begin{pmatrix} c \\ d \end{pmatrix} = \begin{pmatrix} a-c \\ b-d \end{pmatrix}\]

Two-dimensional vectors

3D Subtraction
\[\begin{pmatrix} a \\ b \\ c \end{pmatrix} - \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} a-x \\ b-y \\ c-z \end{pmatrix}\]

Three-dimensional vectors

Geometric Interpretation
\[\vec{a} - \vec{b} = \vec{a} + (-\vec{b})\]

Subtraction as addition of opposite vector

Calculation Examples for Vector Subtraction

Example 1: 2D Subtraction
[3, 5] - [1, 4]
\[\begin{pmatrix} 3 \\ 5 \end{pmatrix} - \begin{pmatrix} 1 \\ 4 \end{pmatrix} = \begin{pmatrix} 3-1 \\ 5-4 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \end{pmatrix}\]

Result: [2, 1]

Example 2: 3D Subtraction
[10, 20, 30] - [1, 2, 3]
\[\begin{pmatrix} 10 \\ 20 \\ 30 \end{pmatrix} - \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 10-1 \\ 20-2 \\ 30-3 \end{pmatrix} = \begin{pmatrix} 9 \\ 18 \\ 27 \end{pmatrix}\]

Result: [9, 18, 27]

Geometric Interpretation
v₁ - v₂
Vector from v₂ to v₁
Not Commutative
a - b ≠ b - a
Parallelogram
Diagonal vector

Subtraction creates the vector from the subtrahend to the minuend

Rules and Restrictions
✓ Allowed

• Same dimension

• Same orientation

• [a,b] - [c,d]

✗ Not Allowed

• Different dimensions

• [a,b] - [c,d,e]

• Row vs column vector

⚠ Notice

• Not commutative

• Order matters

• a - b ≠ b - a

Applications of Vector Subtraction

Vector subtraction is fundamental for movement, differences, and direction calculations:

Navigation & Movement
  • Direction vector between two points
  • Calculate velocity differences
  • Relative movement and position change
  • GPS navigation and pathfinding
Computer Graphics
  • Object movement and transformation
  • Collision detection and avoidance
  • Camera and view transformations
  • Animations and motion interpolation
Physics & Mechanics
  • Force and momentum differences
  • Calculate relative velocities
  • Center of mass and center point
  • Field strengths and potentials
Data Analysis
  • Differences between datasets
  • Trend analysis and change vectors
  • Feature differences in ML
  • Statistical deviation analysis

Vector Subtraction: Differences in Vector Space

Vector subtraction is a fundamental operation of linear algebra that assigns a difference to two vectors. This component-wise subtraction follows the same rules as scalar arithmetic, but elegantly extends them to higher dimensions. Geometrically interpreted, the subtraction v₁ - v₂ creates the vector pointing from the end of the second vector to the end of the first. This operation is central for movement calculations, direction determination, and the analysis of vector differences in physics and engineering.

Summary

Vector subtraction combines algebraic simplicity with geometric significance. The intuitive rule - subtract corresponding components - opens up fundamental spatial relationships between points and directions. From navigation through computer graphics to physics, vector subtraction enables precise calculations of relative positions, movements, and changes. It demonstrates how elementary mathematical operations quantify and make computationally accessible complex spatial and temporal relationships.

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?




Vector Functions

Addition • Subtraction • Multiplication • Scalar Multiplication • Division • Scalar Division • Dot Product • Cross Product • Interpolation • Distance • Distance Squaret • Normalization • Reflection • Magnitude • Squared-Magnitude • Triple-Product